高校数学の参考書、教科書某用問題集、市販問題集の難易度を表にまとめました。
単純にテキストの難易度をまとめただけではなく、大学受験での目標偏差値とテキスト毎の適正偏差値についても考慮してあります。
「ここおかしくね?」とか「このテキストも加えて欲しい!」みたいな要望・質問があれば@hiro_studishまでお願いします。テキストは随時、追加・修正していく予定です。
先に進む前に、必ず以下の項目に目を通してください。ここに掲載されている難易度対照表や適正偏差値は、単純にテキストに掲載されている問題の難易度の幅を表しているわけではないです。あくまでも大学入試に向けて使うとしたらということを考えてあります。
テキストの種類について
テキストは「理解用」「演習用」「入試演習用」「分野別」「計算練習用」の5つに分けて考えるとわかりやすいと思います。
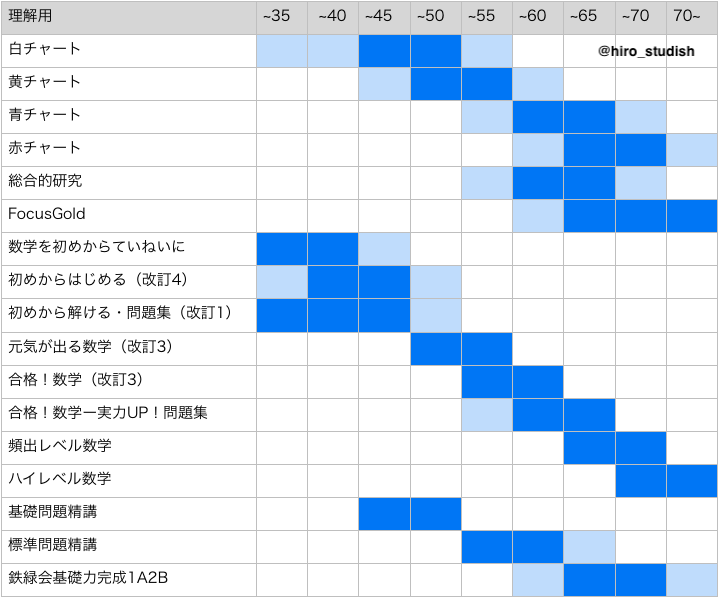
理解用
問題の解き方や考え方を理解するためのテキスト。解説が詳しく載っていて、例題+練習問題の形になっているものが多い。チャートなどが代表例。「理解」というのは演習を通してはじめて完了するものなので、個人的には演習用の問題もセットになっているものが良いと思います。
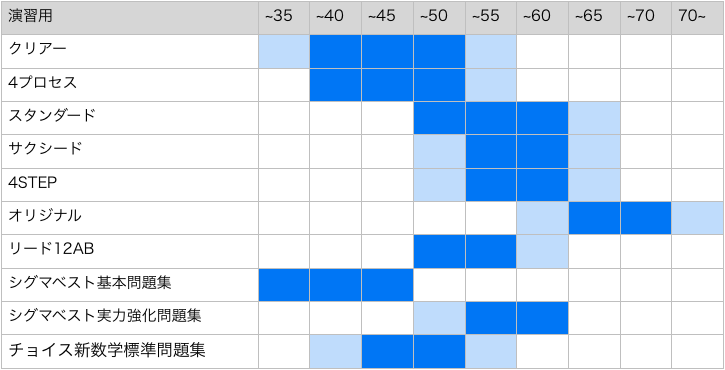
演習用
理解用のみだと演習量が足りないこともあります。そんなときに使うテキスト。問題と解答が別冊になっているものが多く、教科書傍用問題集(例えば4STEP)などが代表例。目標レベルに対しての基本レベルの問題を徹底的に身につけるために使う。
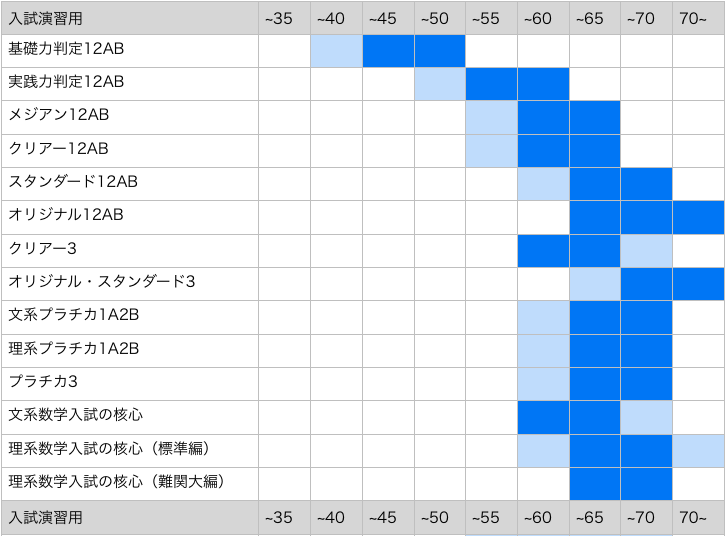
入試演習用
理解用、演習用がある程度身についたあと、一段レベルアップ・仕上げとして使うテキスト。理解用や演習用の知識を使って解く応用的な問題が中心。過去の入試問題からの出題が多い。プラチカなどが代表例。入試演習用は長い間改定されていないものは避けた方が良いと思います。
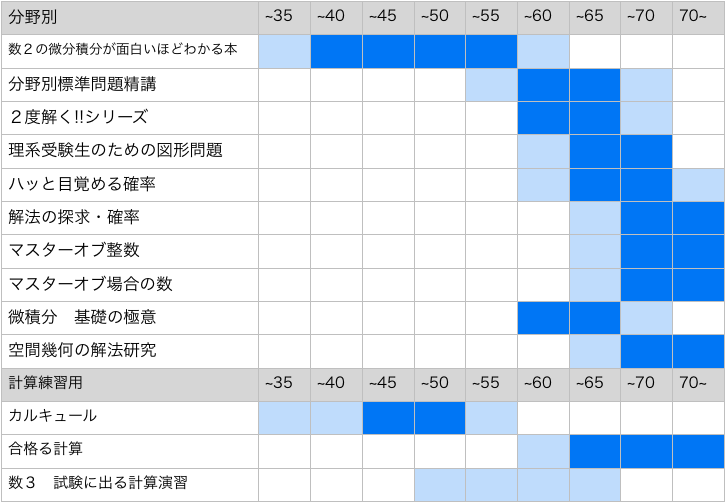
分野別
確率や整数などに単元を絞ったテキスト。弱点を補ったり、出題傾向対策で使うテキスト。「微積分の極意」、「マスターオブ整数」などが代表例。
計算練習用
そのままですが、計算力を強化するためのテキストです。合格る計算などが代表例です。
目標偏差値について
目標偏差値=志望校の偏差値と考えておけばOKです。大学の偏差値については以下のような一般的に言われている値を考えておけばいいと思います。当然、誤差はあるのでざっくりと考えておけばいいでしょう。
70〜:東大、京大、東工大、一橋大、難医大など
65〜70:九大、北大、東北大、阪大、早慶上智など
55〜65:GMARCH、関関同立など
50〜55:日東専駒、産近甲龍など
〜50:大東亜帝国、摂神追桃など
〜40:省略
〜35:高校数学の知識ほぼ0の状態かそれに近い状態
適正偏差値について
理解用と入試演習用
テキストに掲載されている問題の幅だけではなく、そのテキストを最大限活かせる偏差値帯を考慮しました。例えば、FocusGoldは例題は青チャと同じくらいの問題難易度の幅ですが、チャレンジ編や実践編などハイレベルの要素があり、それを活かすことを考えてより高難度の方へ設定しました。また「そのテキストを8〜9割身につけたらどのくらいのレベルになるか?」「目標偏差値〇〇の人に使わせるか?」も考慮し、それらの総合で判断しました。
演習用
演習用は理解用と併せて使うのが基本なので、どの理解用テキストと合わせて使うのが適正かを考え適正偏差値を判断しました。例えばクリアーは白チャや黄チャと合わせて使うのが適正だと思います。
分野別
分野別演習用はどうしても理解できない・弱点になっているところを強化するために使うのを前提とします。その中でも演習用と考えられるものは入試に向けた演習で使うことが多いと思われるので、入試演習用と同じ基準で選びました。一方、理解用と考えられるものはチャートなどと同じ理解用として判断しました。
難易度対照表
表にある「50〜」などの数値は適正偏差値を表しています。濃い青のところが最適な偏差値ゾーンです。薄い青はまあこのくらいの目標偏差値の場合も使っていいかなということを表しています。
難易度対照表はあくまでもそのテキストがどの目標偏差値に適しているかを表したものです。テキストは解説のわかりやすさや見やすさ、使いやすさなども考慮して選んだ方が良いです。
それらテキストの特徴については後述してあるので、どのテキストを使うかはそちらも参考にしてください。


テキストの評価基準
テキストの評価指標として以下の項目を考えました。
・問題数
・難易度
・理解が深まる内容(特筆すべきことがない場合は言及してません)
・別解の有無
・解説のくわしさ、わかりやすさ
・構成のわかりやすさ
掲載してあるテキスト一覧
2017年4月時点で”テキストの特徴”に掲載してあるテキストの一覧です。
色が変わっているところは詳細記事へのリンクになっているので興味ある方はご覧ください。
理解用テキスト一覧
- チャート(チャートは1つの記事にまとめてあります)
- FocusGold
- 総合的研究
- 基礎問題精講
- 標準問題精講
- 数学〇〇をはじめからていねいに
- 初めから始める数学シリーズ
- 元気が出る数学シリーズ
- 合格!数学シリーズ
- 合格数学〇〇実力UP!問題集
- 頻出レベル数学
- ハイレベル数学シリーズ
- 鉄緑会基礎力完成数学1A2B
入試演習用テキスト一覧
- 基礎力判定
- 実践力判定
- 文系プラチカ1A2B
- 理系プラチカ1A2B
- プラチカ3
- 文系入試数学の核心
- 理系入試数学の核心(標準編)
- 理系入試数学の核心(難関大編)
- 入試問題集
- 大学への数学・入試数学の基礎徹底
- 大学への数学・数学3の入試基礎
- 大学への数学・1対1対応の数学
- 大学への数学・新数学スタンダード演習
- 大学への数学・数学3スタンダード演習
- 上級問題精講1A2B
- やさしい理系数学
- ハイレベル理系数学
- 天空への理系数学
- 入試数学の掌握
演習用テキスト一覧
- クリアー
- 4プロセス
- スタンダード
- サクシード
- 4STEP
- オリジナル
- リード
- シグマベスト基本問題集
- シグマベスト実力強化問題集
単元別テキスト一覧
- 数2の微分積分が面白いほどわかる本
- 教科書だけでは足りない
- 分野別 標準問題精講 整数
- 分野別 標準問題精講 場合の数・確率
- 確率が本当によくわかる本
- 合格る確率+場合の数
- ハッとめざめる確率
- マスターオブ場合の数
- マスターオブ整数
- 微積分 基礎の極意
- 大学への数学・解放の探求・確率
- 空間幾何の解放研究
計算練習用テキスト一覧
理解用テキスト
チャート全般のメリット・デメリット
・解説にクセがないので万人向け
・一通り終わったあとで他の問題集を使っている時の辞書として使える
・網羅率は最高クラス
・問題数が多いので完成するのに時間がかかる
各色のチャート式数学の使い方については以下の記事で徹底的に解説してあります。

FocusGold:65〜
・明らかに最難関向け
・例題と練習のレベルは青チャートとほぼ同じ
・StepUpと章末問題のレベルは青チャートのExercisesとほぼ同じ
・チャレンジ編のレベルは青チャートの総合演習と同じ(問題数が違う)
・実践編は明らかに青チャート以上
FocusGoldの詳細は以下の記事をご覧ください。

総合的研究:55〜65
・網羅型
・網羅率はチャートより低い
・1Aの問題数(約):問220題、例題250題、章末問題170題
・とにかく解説が詳しい&丁寧。
・裏を返せば、じっくり取り組む集中力がない人は扱うのが難しいとも言える。
・考察も豊富なのでより深く理解できるのが最大の特徴
・構成がわかりにくいのが最大の難点
・例題の選定が微妙、特に偏差値50前後が薄い印象
・そのかわりにけっこう難しい例題もあったりする
・例題に1対1に対応した例題がない
・問は必ずしも基本的な問題とは限らない
・この構成のせいで演習しにくい
・FocusGoldのチャレンジ編やマスター編のような部分はない
・例題の最大難易度が偏差値55〜60くらい
・章末問題が偏差値50〜65くらい(例題の類題を兼ねている部分あるので幅が広い)
・考察部分が最大の特徴なのでそれを活かすなら目標偏差値60前後の人が使うのがいい
・解説は詳しいし理解が深まる要素はたくさん書いてあるが、構成のわかりにくさや演習のしにくさを考えたら青チャやFocusGoldを使った方がいい
・目標偏差値55未満の人に使わせるかと考えたとき、それなら黄チャかなと思うので適正偏差値の下限を55としました
・目標偏差値65以上の人に使わせるかと考えたとき、それなら赤チャかFocusGoldかなと思うので適正偏差値の上限を65としました
「スバラシク」シリーズ・数学〇〇をはじめからていねいに:〜45
・講義型
・問題数はカウントしにくいのでしてない
・シリーズは数と式・集合と論証・二次関数編、図形と計量・図形の性質編、場合の数・確率・整数の性質・データの分析編、のように分かれている
・偏差値〜45までを1から学ぶことができるのが最大の特徴
・白チャよりさらに下のレベル
・完全に理解用なので演習には向かない
・解説が細かいので数学苦手な人でもわかりやすい
・講義型で少しクセがあるため合わない人は合わない(マセマよりはクセない)
・マセマよりは見やすい
・白チャの例題マーク1つレベルでも解説が難しいと感じる人向け
・センターの問題はたしかに掲載されているが、ところどころ抜き取った形なので実際にはセンター初級レベルといった感じ
・表紙ではセンター適正2重丸ついてますが、じゃあこのテキストでセンター満点取れるかと言われると無理(平均でも難しいのでは?)なので適正偏差値の上限を45としました
「スバラシク」シリーズ・初めから始めるシリーズ(改訂4):〜45
・講義型
・問題数はめんどいのでカウントしてない
・解説は詳しい
・解説が細かすぎて見にくいし逆に使いにくい(個人的な意見)
・問題選定も甘い気がする
・基本レベル(白チャの例題マーク1〜2あたり)の問題は解説がほとんどで演習問題はない(”初めから解ける”の方にある程度掲載されてる)。これはかなりマイナス要素。数学苦手な人は演習を通して理解することが多いので、基本レベルの演習が少ないのは痛い
・完全に理解用なので演習には向かない
・対応問題集と合わせて使って初めて成立するテキストかもしれない
・基本レベルの演習が少ない(解説はあるが)ので適正偏差値の下限を40としました
・問題の最大難易度は白チャの例題と同じくらいなので適正偏差値の上限を45としました
「スバラシク」シリーズ・初めから解ける数学〇〇問題集:〜45
・約140題
・“初めから始める”に対応した問題集
・“初めから始める”の基本レベルにあたる部分の演習問題もある
・講義型ではなくチャートのような構成
・途中式や式変形の解説が詳しい
・講義形式や解説の書き方などの合う合わないはかなり個人差があると思う
・類題もない
「スバラシク」シリーズ・元気が出る数学:45〜55
・初めから始めるシリーズの上位版
「スバラシク」シリーズ・合格!数学シリーズ:50〜60
・元気が出るシリーズの上位版
「スバラシク」シリーズ・合格!数学ー実力UP!問題集:50〜60
・“合格!数学”に対応した問題集
・同じ問題集でも”初めから解ける数学〇〇問題集シリーズ”と少し趣が違う
・こちらはどちらかというと難しい方の問題が厚い
マセマについて(個人的な意見)
・マセマシリーズは主に「理解用」と「演習用(問題集の方)」に分かれる
・「理解用」は講義型で細かく説明してくれている
・途中式やなぜそうしてるのかなどの解説が詳しいのが最大のメリット
・逆にそれ(解説がごちゃごちゃ書かれていて見にくいの)が最大の難点でもある
・そのごちゃごちゃのせいで勉強(数学)が苦手な人は使えないと思われる(やる気があればその点はクリアできるかもしれない
・「演習用」はチャートのような構成だが、類題(練習)やEXERCISESのような問題はない
・マセマシリーズはレベルが細かく分かれているのでレベルに合ったところをピンポイントで選べる
・基本的なことがNGな人が「理解用」を使うのはアリだと思う
・基本的はOKの人が最終目標レベル相当のシリーズを使うのはアリだと思う
・「理解用」だけだと圧倒的に演習量が少ない
・かといって「演習用」が良いかと言われると微妙
・「演習用」だけ進めるのはどうかと言われるとそれならチャート使った方がいい気もする
基礎問題精講:40〜50
・集約型
・1Aの問題数:135題+演習問題135題
・2Bの問題数:167題+演習問題167題
・3の問題数:手元にないので不明
・例題+演習問題という超シンプルな構成なのが特徴
・また、私立の小問対策用という位置付けというのも特徴
・問題パターンも必要最小限に絞ってある
・素早く終わらせられる
・40〜50レベルの土台・軸を作るのに最適
・これだけだと対応できる問題に不安がある
・演習量も足りない
・問題レベルは白チャの例題マーク2〜5くらい
・チャートのEXERCISESのような部分はない
・数学苦手な人は使わない方がいいかもしれない
・時間がない人向け
・より上位を目指すために基本はさらっと流したい人向け(基本はある程度理解してる前提だけど)数学だけに時間をかけたくない人向け(国公立で科目数が多い、国公立文系2次で数学使わないなど)
・小問対策向け
・白チャの例題マーク1〜2つくらいの基本部分が薄いので下限を40としました
・目標偏差値50以上だとちょっと弱いので上限を50としました
標準問題精講:50〜60
・基礎問題精講の上位版
・1Aの問題数:101題+演習問題101題
・2Bの問題数:手元にないので不明
・3の問題数:手元にないので不明
・問題レベルは青チャの例題マーク2〜5くらい
・網羅率は低い
・難関大合格の分かれ目になる問題を掲載していると書いてある。これはつまり合格ラインぎりぎりの問題、マストでとけなければいけないという問題。
・これで偏差値65に受かるかと言われると疑問が残る。
・目標偏差値50以下の人に使わせるかというと、使わせないので下限を50としました
・目標偏差値60以上だとちょっと弱いので上限を60としました
上級問題精講
・標準問題精講の上位版だが構成的に問題集という色が強いので入試演習用に記載してある
鉄緑会基礎力完成数学1A2B:60~
・あくまでも最難関大を目指す人が「基礎力」を身につけるためのテキスト
・掲載されている問題自体は他のテキストでもよくあるものばかり
・最大の特徴は解説編
・解説編は受験で使うテクニックや考え方などがまとまっているので、参考書的に使うと良いと思う
・本来、自分で勉強を進める中で到達する最善ないしそれに近いテクニックや考え方などが書かれているので、これを読みつつ勉強すると効率的に勉強できるかもしれない
・ただし、内容や単元の順序が指導要領通りになっていないので、その点は使いにくい
・問題の解答集は途中計算などが省略されている部分も多いので初心者は使わない方がいい
入試演習用テキスト
基礎力判定:〜50
・1Aは約210題
・2Bは約180題
・12ABまでしかないのが残念
・解説はふつう
・この問題レベルでこういう形式のテキストは珍しい
・学校対策としては使えない
・大学受験勉強をスタートする上での学力チェックにも使える
・これだけだと入試対策としては弱い
・目標偏差値55以上の人に使わせるか考えると、使わせないので適正偏差値の上限を50とした
・目標偏差値50〜55くらいの人が実践力判定と合わせて使うと良い
実践力判定:50〜60
・1Aは約190題
・2Bは約170題
・基礎力判定の上位版
・12ABまでしかないのが残念
・解説はふつう
・この問題レベルでこういう形式のテキストは珍しい
・学校対策としては使えない
・目標偏差値50以下の人に使わせるか考えると、使わせないので適正偏差値の下限を50とした
・目標偏差値60以上の人に使わせるか考えると、使わせないので適正偏差値の上限を60とした
1対1対応の演習:50〜60
1対1対応の演習については以下の記事を参考にしてください
「大学への数学 1対1対応の演習」の難易度とオススメの使い方
新数学スタンダード演習:60〜70
新数学スタンダード演習の詳細は以下の記事をご覧ください。


文系プラチカ12AB:60〜70
・約150題
・解説が詳しいのが最大のメリット
・明らかに難関校向け
・MARCH関関同立の下位学部なら十分すぎる内容
・集約型なので問題パターンは多くない
・理系の人もトレーニングとして使える
・目標偏差値60以下の人に使わせるか考えると、使わせないので適正偏差値の下限を60とした
・目標偏差値70以上だと物足りないので上限を70とした
・時間に余裕があるなら新数学スタンダード演習の方が良い
理系プラチカ12AB:60〜70
・約150題
・解説が詳しいのが最大のメリット
・明らかに難関校向け
・MARCH関関同立の下位学部なら十分すぎる内容
・集約型なので問題パターンは多くない
・目標偏差値60以下の人に使わせるか考えると、使わせないので適正偏差値の下限を60とした
・目標偏差値70以上だと少し物足りない気がするので上限を70とした
・時間に余裕があるなら新数学スタンダード演習の方が良い
理系プラチカ3:60〜70
・手元にないため問題数不明
・解説が詳しいのが最大のメリット
・明らかに難関校向け
・最難関校だと少し足りないかも
・MARCH関関同立の下位学部なら十分すぎる内容
・集約型なので問題パターンは多くない
・目標偏差値60以下の人に使わせるか考えると、使わせないので適正偏差値の下限を60とした
・目標偏差値70以上だと少し物足りない気がするので上限を70とした
・時間に余裕があるなら新数学スタンダード演習の方が良い
文系数学入試の核心:55〜65
・100題
・解説はふつうだが別解や研究が豊富なのは魅力的
・扱うには最低でも青チャの例題を全てクリアしてるくらいの学力は必要
・問題数が少ないので早めに終わらせられる
・問題数が限られてるのでこれだけだと演習不足になるかも
・目標偏差値55以下の人に使わせるか考えると、使わせないので適正偏差値の下限を55とした
・目標偏差値65以上だと少し物足りない気がするので上限を65とした
・プラチカや新数学スタンダード演習の方が良い
理系数学入試の核心(標準編):55〜65
・150題(123AB合わせて)
・解説はふつうだが別解や研究が豊富なのは魅力的
・扱うには最低でも青チャの例題を全てクリアしてるくらいの学力は必要
・問題数が少ないので
・問題数が少ないので早めに終わらせられる
・問題数が限られてるのでこれだけだと演習不足になるかも
・目標偏差値55以下の人に使わせるか考えると、使わせないので適正偏差値の下限を55とした
・目標偏差値65以上だと少し物足りない気がするので上限を65とした
・プラチカや新数学スタンダード演習の方が良い
理系数学入試の核心(難関大編):60〜70
・手元に無いため問題数は不明
・解説はふつうだが別解や研究が豊富なのは魅力的
・扱うには最低でも青チャの例題を全てクリアしてるくらいの学力は必要
・問題数が少ないので早めに終わらせられる
・問題数が限られてるのでこれだけだと演習不足になるかも
・目標偏差値60以下の人に使わせるか考えると、使わせないので適正偏差値の下限を60とした
・目標偏差値70以上だと少し物足りない気がするので上限を70とした
・時間に余裕があるなら新数学スタンダード演習の方が良い
入試問題集数学12AB(文理系):55〜65
・約270題(大問でカウント)
・問題数多いので他の問題集に比べると時間がかかる
・解説はふつう
・他の入試問題集とは構成が異なるので扱い方注意
・単年度の入試問題から有名校の問題を中心に問題を集めてある
・出題パターン毎&難易度順に掲載
・50くらいの問題レベルから掲載されてるが55未満で使えるかと言われるとそうでもない
・実質55〜65くらい向け
・”大学入試問題正解”の簡易版って感じ
・これ使うならスタンダード演習の方が良い
・類題を演習したいときにこのテキストから探してやるみたいな使い方はありかも
入試問題集数学12AB(理系):55〜65
・約270題
・入試問題集数学12AB(文理系)と同じ
入試問題集3:55〜65
・約220題
・入試問題集数学12AB(文理系)と同じ
上級問題精講:65〜
・明らかに最難関校向け
・基礎問題精講、標準問題精講と同じシリーズだが問題集としての色が強いので「入試演習用」に分類した
・1A2Bは約100題(類題除く)
・3は手元にないため問題数不明
・解説はとてもわかりやすい(講義型的な意味ではなく数学的な意味で)
・別解も豊富
・”研究”や”参考(別解)”、類題もあり理解が深まる工夫がされている
・目標偏差値65以下の人に使わせるか考えると、使わせないので適正偏差値の下限を65とした
・時間に余裕があるならハイレベル理系数学や新数学演習の方が良い
やさしい理系数学:55〜65
「やさしい理系数学」の詳細は以下の記事をご覧ください。

ハイレベル理系数学:65〜
「ハイレベル理系数学」の詳細については以下の記事をご覧ください。

天空への理系数学:65〜
「天空への理系数学」の詳細は以下の記事をご覧ください。

入試数学の掌握シリーズ:70〜
「入試数学の掌握」の詳細については以下の記事をご覧ください。

演習用テキスト
リード:45〜55
・塾で使ってるところがたまにある
・手元に無いため問題数は不明
・問題集型
・解説はふつう(途中式が省略されていることもある)。
・マイナーだけどけっこう優れもの。
・1A2Bまでしかないのが残念。
・問題数、パターンが豊富なので基本演習に最適。
・偏差値60くらいまでの高校の学校対策にも最適。
・目標偏差値45以下の人に使わせるかというと、使わせないと思うので下限を45としました
・目標偏差値55以上だとちょっと弱いので上限を55としました
・教科書某用問題集を持っているなら必要ない
シグマベスト基本問題集:〜45
・手元にないため問題数は不明
・問題集型
・解説はふつう
・特にこれといった特徴はない
・目標偏差値45以上の人に使わせるかというと、使わせないので上限を45としました
・教科書某用問題集があるなら必要ない
シグマベスト実力強化問題集:50〜60
・問題集型
・1Aは約570題(旧版の値なので参考までに)
・2Bは約570題(旧版の値なので参考までに)
・3は不明
教科書某用問題集と比較すると問題数は若干少ない(基本的な問題がないため)
解説はふつう
問題選定に多少クセがある(気がする)
結構難しい問題もある
目標偏差値50以下の人に使わせるかというと、使わせないので下限を50としました
目標偏差値60以上だとちょっと弱いので上限を60としました
教科書某用問題集があるなら必要ない
クリアー:35〜50
・1:例題92、大問351
・A:例題79、大問292
・2:例題109、大問492
・B:例題54、大問244
・いわゆる教科書某用問題集
・難易度は白チャより少し上くらい(黄チャよりは下)
・基本知識が0ないしほぼ0の人にはたぶん使わせないので目標偏差値の下限は35としました
・目標偏差値50以上であれば4STEPを使うので上限は50としました
・他の某用問題集は省略
・演習用としてはやはり教科書某用問題集が最も優れている
・教科書某用問題集を持っていなければ市販のもので代用
分野別テキスト
数2の微分積分が面白いほどわかる本(坂田アキラシリーズ):〜55
・約90題
・現状、基本レベルからの分野別で一番有能かもしれない
・ちょっとだけ講義型っぽい
・解説がとても詳しい
・基本から理解するのに最適
・どちらかというと理解用
・坂田アキラシリーズ(数学)には次のテキストがある
・表紙の絵と中の絵が全く違う笑(個人的にはどうでもいいけど)
・図形と方程式が面白いほどとける本
・三角比・平面図形が面白いほどとける本
・確率が面白いほどとける本
・三角関数が面白いほどわかる本
・指数・対数が面白いほどわかる本
・数3の微積が面白いほどわかる本
・数列が面白いほどわかる本
・2次関数が面白いほどわかる本
・数2の微分積分が面白いほどわかる本
分野別標準問題精講:55〜65
「分野別 標準問題精講」についてはそれぞれ以下の記事をご覧ください。


2度解く!!シリーズ:55〜65
・30題
・解説はふつう
・問題とは別にReTryという部分がありますが、問題と全く同じ問題なので意味なし
・適正偏差値としては55〜65くらいの問題が中心
・目標偏差値55未満の人にオススメするかと言われるとしないので下限は55とした
・目標偏差値65以上だと少し物足りないので上限は65とした
シリーズ
・数と式・集合と論理
・2次関数・方程式と不等式
・平面幾何・図形と計量
・確率・順列と組み合わせ
・式と証明・複素数と方程式
・図形と式
・三角関数・指数・対数関数
・微分法と積分法
・数列
・ベクトル
理系受験生のための図形問題(教科書だけでは足りないシリーズ):60〜70
・63題
・解説がとても詳しい
・別解があるのも嬉しい
・目標偏差値60未満の人にオススメするかと言われるとしないので下限は60とした
・目標偏差値70以上だと少し物足りない気もするので上限は70とした
シリーズは以下のものがある
・理系受験生のための図形問題
・整数
・数列
ハッと目覚める確率:55〜70
ハッとめざめる確率の詳細は以下の記事をご覧ください。

解法の探求・確率:60〜
「解法の探求・確率」の詳細は以下の記事をご覧ください。

マスターオブ整数:60〜

マスターオブ場合の数:60〜

微積分 基礎の極意:60〜

空間幾何の解法研究:60〜
・シリーズで無限級数、複素数、式と曲線などがある
・明らかに最難関向け
・聖文新社から出版されてる(と言えばわかる人はわかる)
・過去50年の主要大学(上位国公立、早慶上智あたり)の入試で出題された空間図形に関する問題548題を収録
・解説がとにかく詳しい(図が豊富)
・辞書的に使える
・受験生が個人で使うには冗長すぎる
・空間図形をマスターしたい人にはオススメ
・使うとしても目標偏差値60〜
目次が以下のように分かれているので、的を絞って勉強しやすい
・空間幾何学のための基礎知識
・立体図形の認識と計量
・空間座標と空間ベクトル
・空間図形と方程式
・微積分との融合問題
計算練習用テキスト
カルキュール:〜55

合格る計算:50〜

数3 試験に出る計算演習:50〜
・大学入試でよく出題される数3の計算問題を集めた問題集です
・「試験によく出る」というのはあくまでも大学入試の2次試験という意味であって、学校の試験ではないです
・受験生が勉強の進度に合わせて使うのがオススメ
・または受験生が数3を一通り勉強した後、入試演習用の問題集に入る前に使うのがオススメ
・偏差値55〜の大学入試の場合は計算できて当たり前になってくるので、そういう意味で使うと良いでしょう
・偏差値〜55の大学入試の場合は計算問題が単独で出題されることもあるので、そういう意味で使うといいでしょう
・使い所が難しいですが、使い方さえちゃんとしてれば結構良い問題集だと思います
・数3の計算だけ、しかも入試問題がまとまってるものはあまり見かけないですし
・学校対策や入試基礎固めだったらカルキュールが良いですね
以上です。教材は順次追加していきます。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。