スタンダード数学演習12AB-2018

スタンダード数学演習12AB（2018）の解説　312

  /
2018スタンダード数学演習12AB

スタンダード数学演習12AB（2018）、「ベクトルの基本」のA問題312の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。

回答例の「方針」や（ ）内の説明は実際の回答ではないですが、解説のために入れてあります。

 

(1)の回答例

方針：セオリーどおり、\vec{PQ}を他のベクトルで表していく。

 

（まずは図を書きましょう）

Rendered by QuickLaTeX.com

 

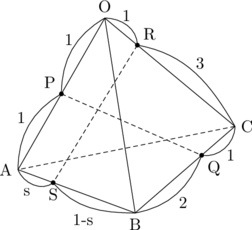
(1)   \begin{eqnarray*} \vec{PQ}&=&\vec{OQ}-\vec{OP}\\ &=&\frac{\vec{b}+2\vec{c}}{3}-\frac{\vec{a}}{2}\\ &=&-\frac{1}{2}\vec{a}+\frac{1}{3}\vec{b}+\frac{2}{3}\vec{c} \end{eqnarray*}

 

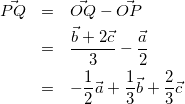
(2)の回答例

方針：(1)と同様にセオリーどおり、\vec{RS}をsと他のベクトルで表していく。

 

(2)   \begin{eqnarray*} \vec{RS}&=&\vec{OS}-\vec{OR}\\ &=&(1-s)\vec{a}+s\vec{b}-\frac{1}{4}\vec{c} \end{eqnarray*}

 

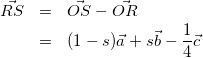
(3)の回答例

方針：交点をTとして、\vec{PT}を2通りで表して係数比較する方向で考える。

 

線分PQと線分RSの交点をTとする。

(3)   \begin{eqnarray*} \vec{PT}&=&k\vec{PQ}\\ &=&-\frac{1}{2}k\vec{a}+\frac{1}{3}k\vec{b}+\frac{2}{3}k\vec{c} \end{eqnarray*}

 

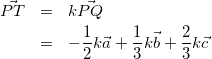
また、tを実数として

(4)   \begin{eqnarray*} \vec{PT}&=&\vec{PR}+\vec{RT}\\ &=&\vec{OR}-\vc{OP}+t\vec{RS}\\ &=&\frac{1}{4}\vec{c}-\frac{1}{2}\vec{a}+t(1-s)\vec{a}+st\vec{b}-\frac{1}{4}t\vec{c}\\ &=& \left\{ t(1-s)-\frac{1}{2} \right\}\vec{a}+st\vec{b}+\frac{1}{4}(1-t)\vec{c} \end{eqnarray*}

 

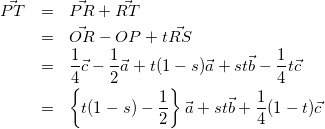
式(3)(4)を係数比較して

(5)   \begin{eqnarray*} -\frac{1}{2}k&=&t(1-s)-\frac{1}{2} \hspace{1cm} \cdots \textcircled{\scriptsize 1}\\ \frac{1}{3}k&=&st \hspace{2cm} \cdots \textcircled{\scriptsize 2}\\ \frac{2}{3}k&=&\frac{1}{4}(1-t) \hspace{1cm} \cdots \textcircled{\scriptsize 3} \end{eqnarray*}

 

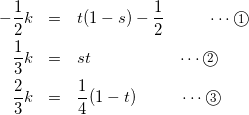
式(5)-②より

(6)   \begin{eqnarray*} k=3st\\ \end{eqnarray*}

 

これを式(5)-①に代入して

(7)   \begin{eqnarray*} -\frac{3}{2}st&=&t-st-\frac{1}{2}\\ -3st&=&2t-2st-1\\ st+2t-1&=&0 \end{eqnarray*}

 

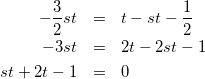
また、式(5)-③にも代入して

(8)   \begin{eqnarray*} 2st&=&\frac{1}{4}(1-t)\\ 8st&=&1-t\\ 8st+t-1&=&0 \end{eqnarray*}

 

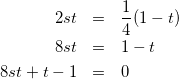
式(7)×8 ー 式(8)より

(9)   \begin{eqnarray*} 15t-7&=&0\\ t&=&\frac{7}{15} \end{eqnarray*}

 

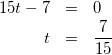
これを式(5)-③に代入して

(10)   \begin{eqnarray*} \frac{2}{3}k&=&\frac{1}{4}\left(1-\frac{7}{15}\right)\\ \frac{2}{3}k&=&\frac{1}{4}\cdot\frac{8}{15}\\ k&=&\frac{1}{5} \end{eqnarray*}

 

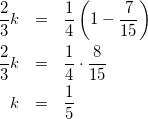
求めたtとkの値を式(5)-②に代入して

(11)   \begin{eqnarray*} \frac{1}{3}\cdot\frac{1}{5}&=&s\cdot\frac{7}{15}\\ s&=&\frac{1}{7} \end{eqnarray*}

 

 

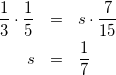
(1)のポイント

図を書けば自然と式を作れるはず。図を描いても\vec{OQ}-\vec{OP}などの式を思いつかない人は演習不足なので、練習しておこう。

また、以下の内分点を表すベクトルの式の作りかたも基本なのですぐに反応できるようにしておこう。

    \begin{eqnarray*} \vec{OQ}&=&\frac{\vec{OB}+\vec{OC}}{3}\\ &=&\frac{\vec{b}+\vec{c}}{3}\\ \end{eqnarray*}

 

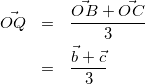
(2)のポイント

(2)も(1)と同じ。

 

(3)のポイント

(3)は正解ルートが見えにくいが、セオリーどおりに式を作っていき、正解ルートを探していくのがポイント。

ここでのセオリーは「sの値を求めたいので、式を2つ（1つはsを絡ませた式）作って係数比較する」こと。

また、2つ式を作ったときに、与えられたベクトルが3つあることから、「未知数が3つあっても3つのベクトルの係数を比較することでその未知数を求められそうだな」と思えるかどうかもポイントになる。

基本的に「未知数の数と式の数が同じであれば、連立方程式として解ける」というのはめちゃくちゃよく使う知識なので覚えておこう。

 

闇雲に進んで解けないと時間の無駄になってしまう。入試は時間との勝負なので、解いている途中で少し手を止めて、見通しを立てる習慣をつけることをおすすめします。

オンライン指導、生徒受付中！

神奈川県公立高校入試、都立高校入試、大学入試で個別指導20年、オンライン指導9年の私がマンツーマンで丁寧に指導します。

  • 対象学年：中学生、高校生、浪人生
  • 指導科目（高校）：数学、物理、大学受験指導
  • 指導科目（中学）：数学、理科、高校受験指導
  • 指導形態：SkypeまたはZoomによるオンライン指導
  • 指導曜日・時間：要相談
  • 料金：1時間7,000円（税別）
  • 体験指導：60分（ヒアリング含む）

 

体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

お問い合わせ

関連記事

COMMENT

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

CAPTCHA