オンライン講師ブログ

スタンダード数学演習12AB-2018

スタンダード数学演習12AB（2018）の解説　311

online-tutor 2018年6月19日 / 2018年10月19日

2018スタンダード数学演習12AB

スタンダード数学演習12AB（2018）、「ベクトルの基本」のA問題311の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。

回答例の「方針」や（）内の説明は実際の回答ではないですが、解説のために入れてあります。

(1)の回答例

方針： $\vec{PB}$ 、 $\vec{PC}$ 、 $\vec{PD}$ をそれぞれ他のベクトルで表すことを考える

（まずは図を書きますが、その前に問題全体に目を通すとPの位置が絞られるので図が書きやすくなります。）

Rendered by QuickLaTeX.com

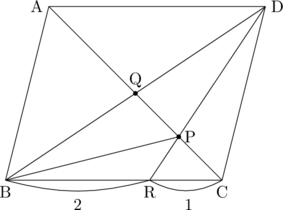
（問題を(1)〜(3)まで読めばこんな感じの図が書けると思います。線分BDや線分BPは最初の時点では引くことを思いつかないかもしれません。）

(1) $\begin{eqnarray*} \vec{PB}=\vec{AB}-\vec{AP} \end{eqnarray*}$

(2) $\begin{eqnarray*} \vec{PC}=\vec{AC}-\vec{AP} \end{eqnarray*}$

(3) $\begin{eqnarray*} \vec{PD}&=&\vec{PC}+\vec{CD}\\ &=&\vec{AC}-\vec{AD}-\vec{AB} \end{eqnarray*}$

式(1)(2)(3)より

(4) $\begin{eqnarray*} \vec{PB}+\vec{PC}+\vec{PD}&=&\vec{AB}-\vec{AP}+\vec{AC}-\vec{AP}+\vec{AC}-\vec{AD}-\vec{AB}\\ &=&2\vec{AC}-3\vec{AP} \end{eqnarray*}$

(2)の回答例

方針： $\vec{AP}=k\vec{AC}$ と表すことことを考える

(1)より、

(5) $\begin{eqnarray*} \vec{PB}+\vec{PC}+\vec{PD}=r\vec{PA}&=&2\vec{AC}-3\vec{AP}\\ -r\vec{AP}&=&2\vec{AC}-3\vec{AP}\\ (3-r)\vec{AP}&=&2\vec{AC}\\ 3-r&\neq0&\\ \vec{AP}&=&\frac{2}{3-r}\vec{AC} \end{eqnarray*}$

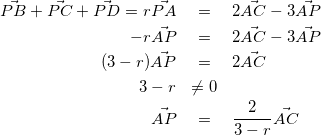
-1≦r≦1より、

(6) $\begin{eqnarray*} 2\leqq 3-r \leqq 4\\ \frac{1}{4}\leqq \frac{1}{3-r} \leqq \frac{1}{2}\\ \frac{1}{2}\leqq \frac{2}{3-r} \leqq 1 \end{eqnarray*}$

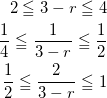
よって、PはQC上の点である。

(3)の回答例

方針：D、P、Rが一直線上にある　→　 $\vec{DP}=k\vec{DR}$ から考えはじめる。

D、P、Rが一直線上にあるのでkを実数として、

(7) $\begin{eqnarray*} \vec{DP}&=&k\vec{DR}\\ &=&k\frac{\vec{DB}+2\vec{DC}}{3}\\ &=&\frac{k}{3}\vec{DB}+\frac{2}{3}k\vec{DC}} \end{eqnarray*}$

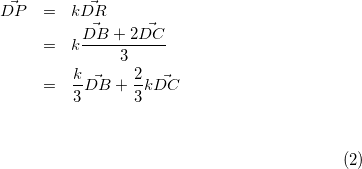
また、(2)より

(8) $\begin{eqnarray*} \vec{DP}&=&\vec{AP}-\vec{AD}\\ &=&\frac{2}{3-r}\vec{AC}-\vec{AD}\\ &=&\frac{2}{3-r}(\vec{AD}+\vec{DC})-\vec{AD}\\ &=&\frac{r-1}{3-r}\vec{AD}+\frac{2}{3-r}\vec{DC}\\ &=&\frac{r-1}{3-r}\vec{BC}+\frac{2}{3-r}\vec{DC}\\ &=&\frac{r-1}{3-r}(\vec{DC}-\vec{DB})+\frac{2}{3-r}\vec{DC}\\ &=&\frac{r+1}{3-r}\vec{DC}-\frac{r-1}{3-r}\vec{DB}\\ &=&\frac{1-r}{3-r}\vec{DB}+\frac{r+1}{3-r}\vec{DC} \end{eqnarray*}$

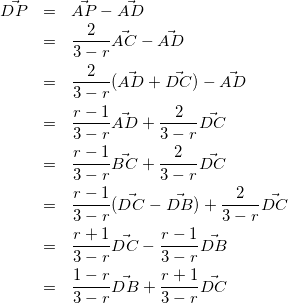
式(7)(8)の係数を比較して、

(9) $\begin{eqnarray*} \frac{1}{3}k=\frac{1-r}{3-r} \hspace{1cm}\cdots\textcircle{\scriptsize 1}\\ \frac{2}{3}k=\frac{1+r}{3-r}\hspace{1cm}\cdots\textcircle{\scriptsize 2}\\ \end{eqnarray*}$

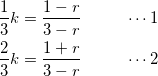
式(9)-②より

(10) $\begin{eqnarray*} \frac{1}{3}k=\frac{1+r}{2(3-r)} \end{eqnarray*}$

式(9)-①と式(10)より、

$\begin{eqnarray*} \frac{1-r}{3-r}=\frac{1+r}{2(3-r)} \end{eqnarray*}$

3-r≠0なので、

(11) $\begin{eqnarray*} 1-r&=&\frac{1+r}{2}\\ 2-2r&=&1+r\\ 3r&=&1\\ r&=&\frac{1}{3} \end{eqnarray*}$

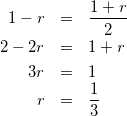
(1)のポイント

うまいこと $\vec{AB}$ が消えるように式変形するのがポイントだが、実際に解くときには一発で思いつくのは難しいので、色々試してみることが重要。

とりあえず、 $\vec{PB}$ 、 $\vec{PC}$ 、 $\vec{PD}$ を $\vec{AP}$ や $\vec{AC}$ を含む形に変形してみる。

そうすれば「邪魔なベクトルを消去するにはどうしたらいいか、考えればいいじゃん！」と次のアイデアに進むことができるかもしれない。

(2)のポイント

問題文を読んで、(1)の結果を利用することに気づけば途中まではさらっといけるはず。あとは $\frac{1}{2} \leqq \frac{2}{3-r}\ \leqq 1$ を確かめることを忘れないこと。記述でこれを忘れると減点どころか不正解とされる可能性も十分ある。

その理由は、点Pが線分QC上の点である条件は $\frac{1}{2} \leqq \frac{2}{3-r}\ \leqq 1$ なので、その手前までだと、A、P、Cが同一直線上にあることまでしか示せていないから。

(3)のポイント

まずはD、P、Rが同一直線上であることから $\vec{DP}=k\vec{DR}$ を利用することを思いつくかどうかがポイント。

この、「A、B、Cの3点が同一直線上にある」→「 $\vec{AB}=k\vec{AC}$ 」というのは基本知識なので、すぐに反応して立式できるようにしておこう。

この流れで $\vec{DP}$ が $\vec{DB}$ と $\vec{DC}$ で表されるのを確認したら、「もう一つ $\vec{DP}$ の式を $\vec{DB}$ と $\vec{DC}$ を使って表して、係数比較すればいいじゃん！」と反応できるかどうかもポイント。

少し難しいが「2つの式を作って係数比較する」のも、基本知識なのですぐに反応できるレベルになるまで類題演習をしよう。

2つ目の $\vec{DP}$ の式を変形していき、rと $\vec{DB}$ と $\vec{DC}$ だけにするのは試行錯誤するしかない。回答例よりもうまく式変形する方法もあるかもしれない。

一応、私の考えたことを書いておく。

とりあえず 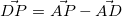$\vec{DP}=\vec{AP}-\vec{AD}$ で考えてみるか
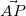$\vec{AP}$ を(2)を使って変形してみるか
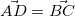$\vec{AD}=\vec{BC}$ が使えそうだ
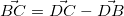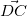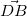なぜなら、 $\vec{BC}=\vec{DC}-\vec{DB}$ なので、欲しい $\vec{DC}$ と $\vec{DB}$ が出現するから

こんな感じですね。

オンライン指導、生徒受付中！2月3月に指導開始の場合、割引！

神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。

対象学年：中学生、高校生、浪人生
指導科目（高校）：数学、物理、大学受験指導
指導科目（中学）：数学、理科、高校受験指導
指導形態：SkypeまたはZoomによるオンライン指導
指導曜日・時間：要相談
料金：1時間6,000円（税別）→5,000円（2月3月指導開始の方だけ！）
体験指導：60分（ヒアリング含む）

体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

お問い合わせ

COMMENT コメントをキャンセル