スタンダード数学演習12AB(2018)、「ベクトルと平面図形(1)」のA問題323の解説です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。
回答例の「方針」や( )内の説明は実際の回答ではないですが、解説のために入れてあります。
(1)の回答例
方針:セオリー通りでOK。![]() という式があるが、この式を変形して両辺を2乗すると?
という式があるが、この式を変形して両辺を2乗すると?
(1) 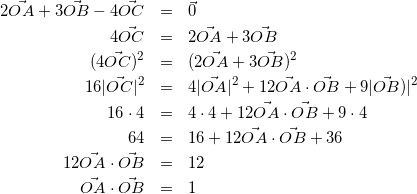
(2)の回答例
方針:セオリー通り、![]() を既存のベクトルで表してみるところからスタート。あとは(1)の結果を利用することも考えるとよりスムーズになる。
を既存のベクトルで表してみるところからスタート。あとは(1)の結果を利用することも考えるとよりスムーズになる。
(2) ![]()
(![]() 、
、![]() 、
、![]() はすでにわかっているので
はすでにわかっているので![]() の計算結果は数値で表せる。)
の計算結果は数値で表せる。)
(3) 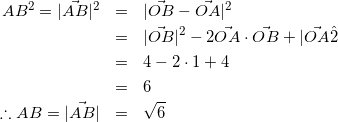
(3)の回答例
方針:これもセオリー通り。![]() を2通りで表して係数比較すればOK。
を2通りで表して係数比較すればOK。
(まずは図を書いてみましょう。)
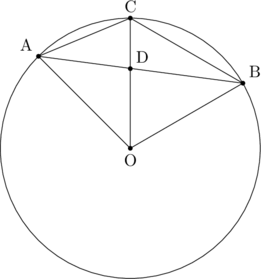
(4) 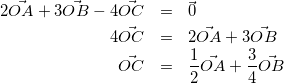
なので、kを実数として、
(5) 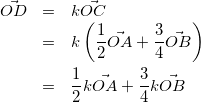
また、点Dは線分ABをs:1-sに内分する点と考えられるので、
(6) ![]()
式(5)と式(6)の係数を比較して
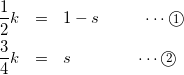
式②を式①に代入して
(7) 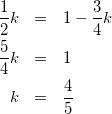
式(7)を式(5)に代入して
(8) 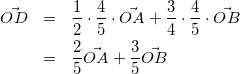
(4)の回答例
方針:△OACと△OBCに分けて考えて、とりあえずそれぞれの面積を計算してみる。
(9) 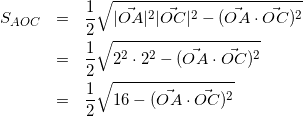
(![]() が必要。セオリー通り、
が必要。セオリー通り、![]() は(4)の式を使って
は(4)の式を使って![]() と
と![]() で表すことができるので・・・)
で表すことができるので・・・)
(10) 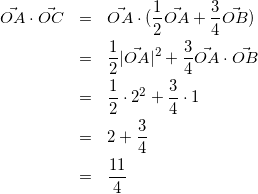
式(10)を式(9)に代入して
(11) 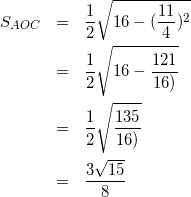
(△BOCも同様に考える)
(12) 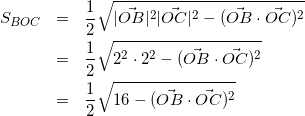
(13) 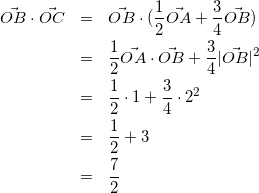
式(13)を式(12)に代入して
(14) 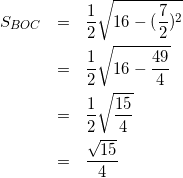
よって、式(11)と式(14)より
(15) 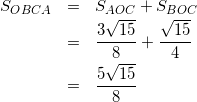
(1)のポイント
この問題のような条件式が与えられた場合、回答例のような式変形はよく使うので覚えておくといいでしょう。
(16) 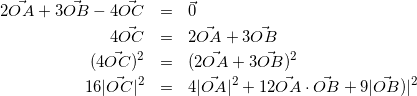
計算結果には3つのベクトルの絶対値の2乗と内積が出てくる。このうち「3つの値がわかっていればこの方程式は解ける」という感覚を身につけることが大切ですね。
(2)のポイント
「扱いにくいベクトルを扱いやすいベクトルに置き換える」というのはベクトルの問題でのセオリーなので反応できるようにしておきましょう。
今の場合、![]() を問題文の中で使われている
を問題文の中で使われている![]() と
と![]() で表すことを考えればOKです。
で表すことを考えればOKです。
この問題の場合は図形を書けばすぐに思いつくと思います。
さらに、(1)と同様に「2乗すれば良さげ」と反応できるかどうかもポイント。この計算は本当によく使いますね。
(3)のポイント
「2通りのベクトルで表して係数比較」もベクトルの問題ではよく使う解き方です。
慣れないうちは、kを使って![]() のように表すのは違和感があると思います。
のように表すのは違和感があると思います。
「この式作って解けるの?」って感じですよね。
慣れてくれば「係数比較すれば解ける!」という感覚に変わってきます。その感覚になるまで練習しましょう。
(4)のポイント
円の内部にある四角形の面積を求める問題では、「2つの三角形に分割して考える」というのはセオリーですね。
あとは、「とりあえず計算してみよう」と思って式を作っていくことが重要です。
それぞれの面積を求めるときにも(1)や(2)のポイントで解説した「扱いやすいベクトルに置き換える」というセオリーを使っています。
△AOCと△BOCの面積を求める過程で![]() や
や![]() 出てきますが、ここで「(3)でどっちも出てきたな」と反応できるかどうかもポイントです。
出てきますが、ここで「(3)でどっちも出てきたな」と反応できるかどうかもポイントです。
「どうせ(1)〜(3)の結果を使うんだろ」という意識を持っていればそこにも気づきやすくなりますね。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

