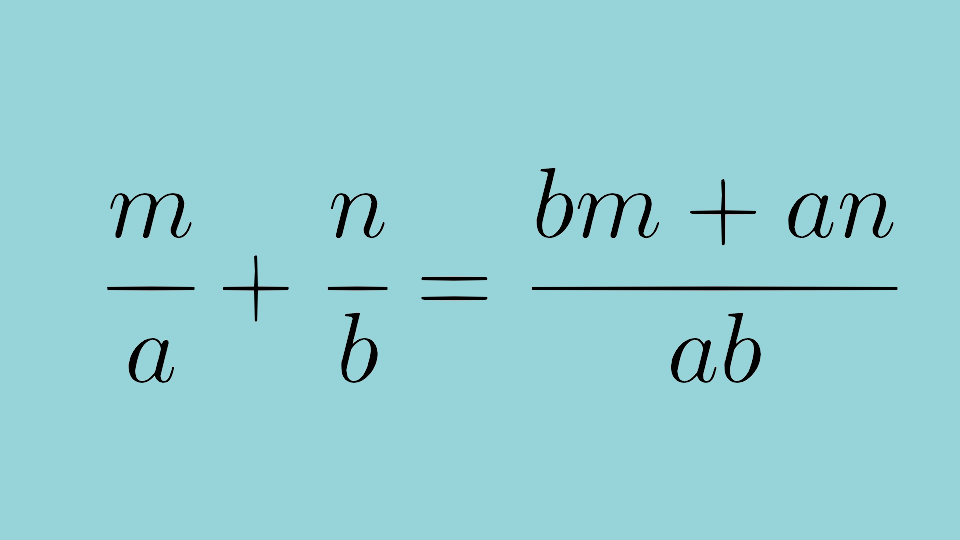問題作成してて、計算結果が約分できる形の2つの分数の和を考えるのって結構面倒だと思ったので、そうなる既約分数の条件を考えてみました。これで問題作成も捗るはず。
どんな問題を作りたいかというとこんな感じ。
![]()
- a、bは互いに素
- mがaの倍数ではない
- nがbの倍数ではない
の場合を考える。上の条件2と3は要するに、2つの分数が既約分数であるってことです。この場合、この分数が約分できる条件は以下の通り。
![]() が
が![]() の倍数、または
の倍数、または![]() の倍数
の倍数
![]()
![]() が
が![]() の倍数、または
の倍数、または![]() が
が![]() の倍数
の倍数
これはそれぞれ条件2、3に反するので不適。
つまり、aとbが互いに素の場合は不適。逆に言えば、分母に共通因数を含めばイケる。
![]()
この場合、約分できる条件は以下のようになるはず。
![]() が
が![]() の倍数
の倍数
これは、![]() が偶数か奇数かによって分けて考えるとわかりやすそう。
が偶数か奇数かによって分けて考えるとわかりやすそう。![]() が偶数の場合の方が簡単。
が偶数の場合の方が簡単。
![]() が偶数の場合、
が偶数の場合、
![]() が
が![]() の倍数
の倍数
![]()
![]() が偶数
が偶数
![]()
![]() が偶数かつ
が偶数かつ![]() が偶数、または、
が偶数、または、![]() が奇数かつ
が奇数かつ![]() が奇数
が奇数
最初の条件から![]() と
と![]() は偶数ではない、つまり奇数なので、
は偶数ではない、つまり奇数なので、
![]() が偶数かつ
が偶数かつ![]() が偶数、または、
が偶数、または、![]() が奇数かつ
が奇数かつ![]() が奇数
が奇数
![]()
![]() と
と![]() が互いに素な奇数、かつ、
が互いに素な奇数、かつ、![]() と
と![]() が互いに素な奇数
が互いに素な奇数
例えば、以下のような分数。
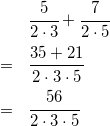
![]() が奇数の場合は少し複雑だけど、
が奇数の場合は少し複雑だけど、
![]()
この式を満たすための条件は、以下のところまでしか絞り込めない。
![]() が
が![]() の倍数
の倍数
これを満たす、![]() はいくつも組み合わせが考えられるが、要するに
はいくつも組み合わせが考えられるが、要するに![]() の1次不定方程式をとけば良いってことですね。
の1次不定方程式をとけば良いってことですね。
例えば、![]() 、
、![]() 、
、![]() の場合
の場合
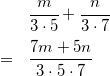
これが約分できるためには、![]() が
が![]() の倍数であれば良いので、
の倍数であれば良いので、
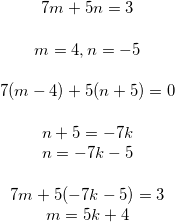
例えば、![]() の場合、
の場合、
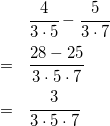
![]() が偶数の場合でも奇数の場合でも、
が偶数の場合でも奇数の場合でも、![]() 、
、![]() 、
、![]() の値を決めれば
の値を決めれば![]() 、
、![]() の条件も定まりますね。1次不定方程式を解けば、あとは
の条件も定まりますね。1次不定方程式を解けば、あとは![]() のを変えるだけで、簡単に条件に合った分数が求まるのも便利ですね。分母や分子の因数を変えれば色々な組み合わせが作れます(たぶん)。
のを変えるだけで、簡単に条件に合った分数が求まるのも便利ですね。分母や分子の因数を変えれば色々な組み合わせが作れます(たぶん)。
元々は問題作成のために考えた内容なので、分母、分子が2桁の分数のリストでも作っておこうかな。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。