小学校で分数の割り算を習うときに、「逆数をかける」と教わると思いますが、その理由を答えられますか？数学では「そういうルールだから」と細かい説明をされずにスルーしていることがよくありますが、今回はその１つを解決しておきましょう。
10÷2の意味は？
「なぜ逆数をかけるのか」を理解するためにはまず割り算を理解しなければいけません。例えば10÷2は計算すれば、その答えは5と誰でもわかりますが、果たしてその意味はわかるでしょうか？
「計算に意味なんてない！」と言う人もいると思いますが、ここでは例えば具体例をあげるとすればどうなるか、と考えてもらえると良いと思います。
私が生徒に説明するときはこの二つをよく使います。
- 10の中に2がいくつ含まれているか
- 10を2個ずつに分けたらいくつに分けられるか
①の考えをもとにすると「なぜ逆数をかけるのか」を簡単に理解することができます。
1÷1/5=1×5？
まずは分子が1の場合を考えましょう。まずは上記①の考え方で理解してみましょう。
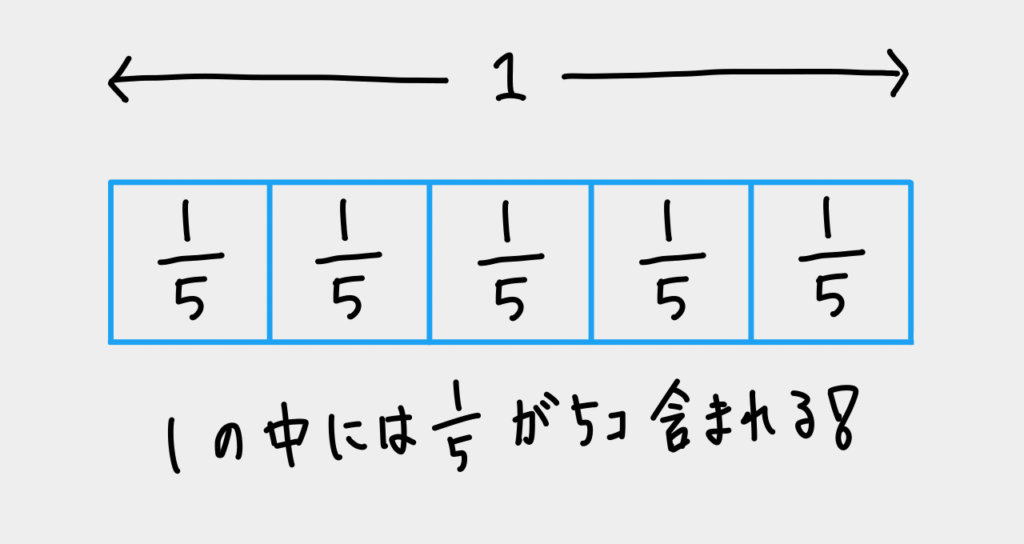
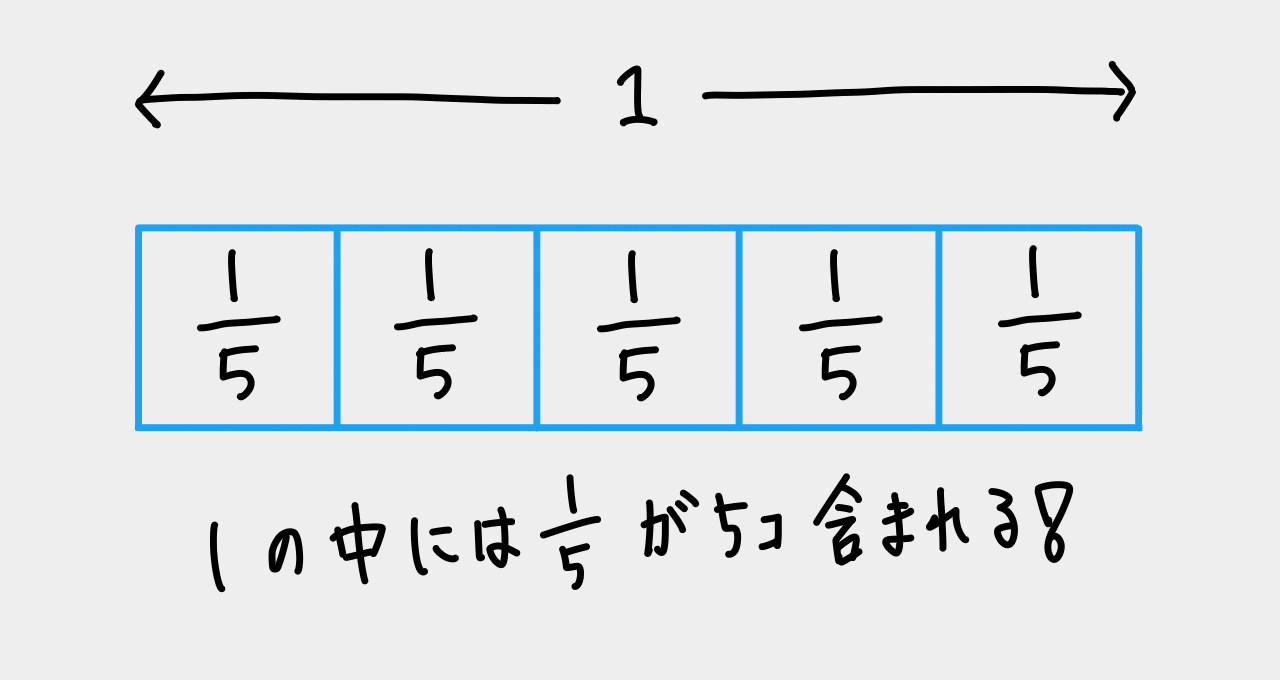
上記①の考え方をベースにすると 
は、「1の中に
がいくつ含まれるか」と考えれば良いので、答えは5個になるというのは直感的にわかりやすいですね（上記画像見るとわかりやすいですね）。
②もほぼ同じように考えられます。「1を ずつに分けたらいくつに分けられるか？」を考えれば良いので、上記①と同じ図で考えられるのがわかると思います。
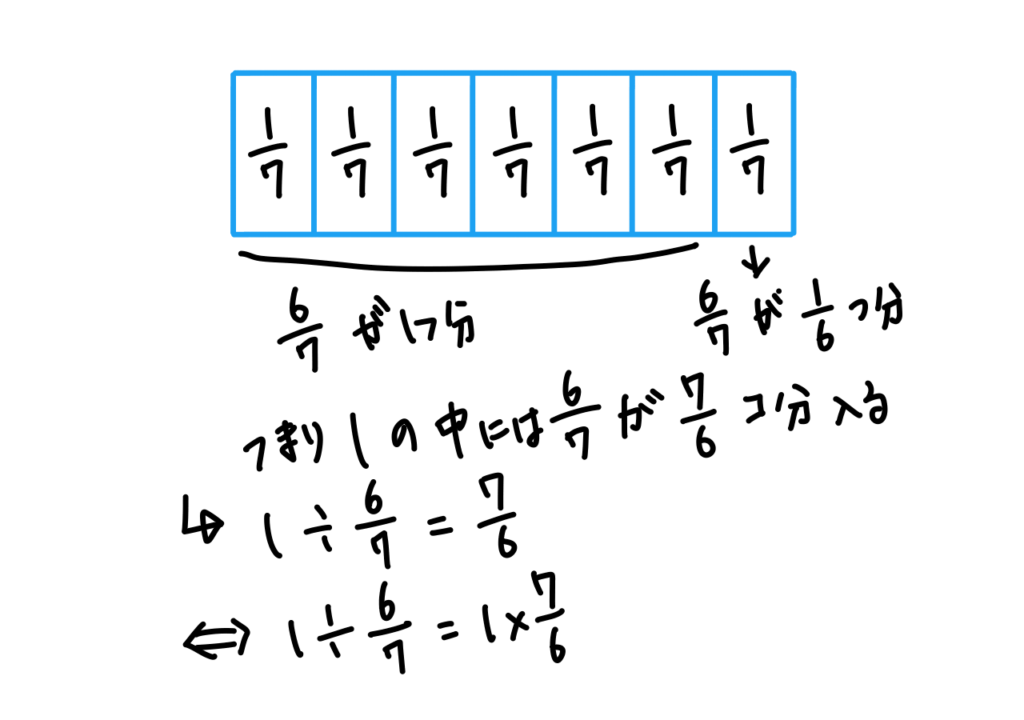
1÷6/7=1×7/6？
これも前項目と同じように考えることができます。
3/5÷6/7
最後は分数を分数で割る計算ですが、これはここまでの考え方を利用すれば計算的に理解することができます。
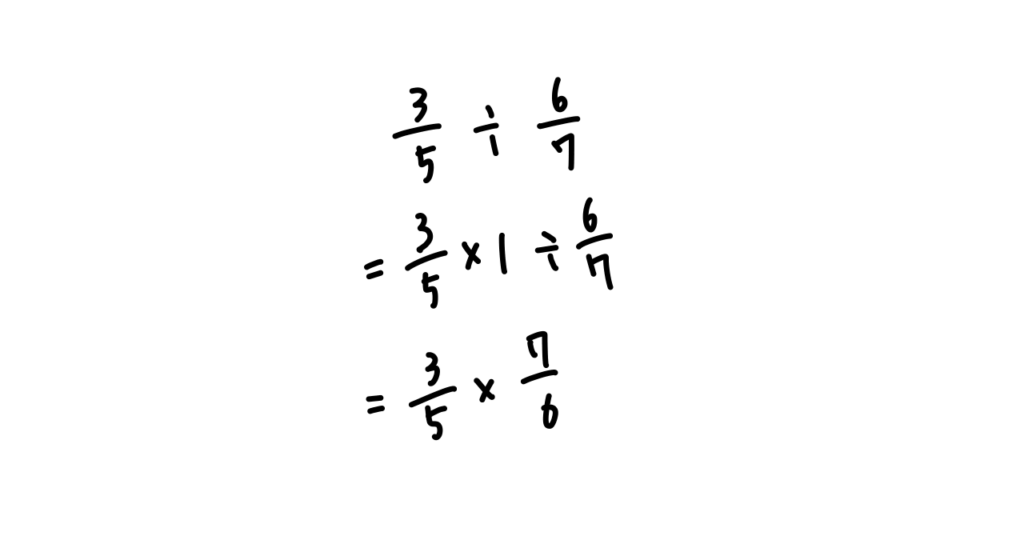
割り算は掛け算で表せる
このように、「かける逆数にする」ことの本質は「割り算は掛け算で表せる」ことにあります。単位あたりの量に変換して考えることで、それがわかりやすくなります。
こういう本質的だけど「そういうものだから」と流されていることって中学や高校よりも小学校内容の方が多いんですよね。説明するのが難しいし、説明しても理解できない生徒の方が多いからだと思いますが。
今回の解説は「超・面白くて眠れなくなる数学」でも解説がされているので、興味がある方は読んでみてはいかがでしょうか。この記事とは異なる解説例が載っているので、より理解が深まると思います。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年：中学生、高校生、浪人生
- 指導科目（高校）：数学、物理、大学受験指導
- 指導科目（中学）：数学、理科、高校受験指導
- 指導形態：SkypeまたはZoomによるオンライン指導
- 指導曜日・時間：要相談
- 料金：1時間6,000円（税別）→5,000円（2月3月指導開始の方だけ！）
- 体験指導：60分（ヒアリング含む）
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。
