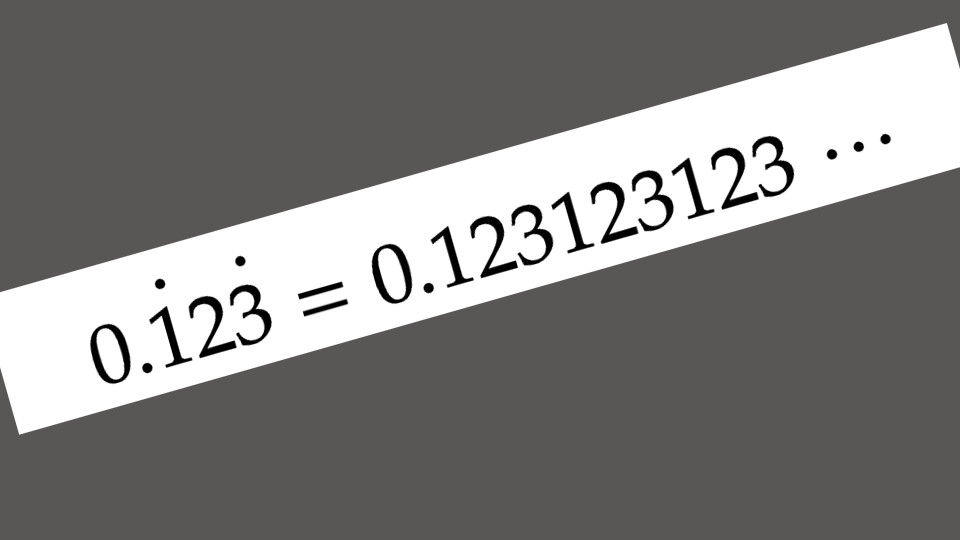循環小数を因数分解してみた。｜オンライン講師ブログ

数１で「循環小数を分数で表す。」ってのをやると思いますが、今回はそれとは異なり、循環小数を因数分解してみました。

問題　 $0.\dot{1} 2 \dot{3}$ を因数分解しなさい。

パッと見、方針を立てにくいかもしれませんが、循環する部分をうまく利用して因数分解します。以下、回答例ですが、回答例を見る前に自分で考えてみてください。

回答例

$\begin{eqnarray*} 0.\dot{1}2\dot{3}&=&0.123123123\cdots\\ &=&123\left(\frac{1}{10^3}+\frac{1}{10^6}+\frac{1}{10^9}+\cdots+\frac{1}{10^{3n}}\right)\\ &=&123 \cdot \sum_{k=1}^{n} \frac{1}{10^{3k}}\\ &=&123\cdot \frac{1}{10^3} \cdot \frac{1-(10^{-3})^n}{1-10^{-3}}\\ &=&\frac{123}{999} \cdot \frac{10^{3n}-1}{10^{3n}}\\ &=&\frac{123}{999} \cdot \frac{1}{10^{3n}} \cdot (10^{n}-1)(10^{2n}+10^n+1)\\ &=&\frac{41}{333} \cdot \frac{1}{10^{3n}} \cdot (10^{n}-1)(10^{2n}+10^n+1)\\ \end{eqnarray*}$

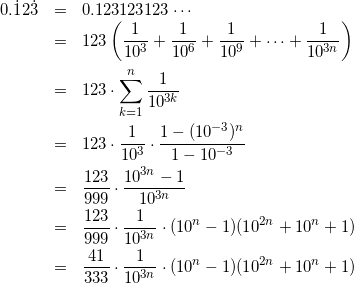
これで因数分解終了です。

一応、n=1,2の場合を確認しておきましょう。

$\begin{eqnarray*} n=1 &&\frac{41}{333} \cdot \frac{1}{10^{3}} \cdot (10-1)(10^{2}+10+1)\\ &=&\frac{41}{333} \cdot \frac{1}{10^{3}} \cdot 9 \cdot 111\\ &=&\frac{123}{1000}\\ &=&0.123 \end{eqnarray*}$

$\begin{eqnarray*} n=2 &&\frac{41}{333} \cdot \frac{1}{10^{6}} \cdot (10^2-1)(10^{4}+10^2+1)\\ &=&\frac{41}{333} \cdot \frac{1}{10^{6}} \cdot 99 \cdot 10101\\ &=&\frac{41}{333} \cdot \frac{1}{10^{6}} \cdot 3^2\cdot11\cdot 3\cdot37\cdot91\\ &=&\frac{123}{10^6} \cdot 1001\\ &=&\frac{123}{10^6} \cdot (1000+1)\\ &=&123 \left( \frac{1}{10^6} \cdot 1000+\frac{1}{10^6} \cdot 1 \right)\\ &=&123 \left( \frac{1}{10^3}+\frac{1}{10^6} \right) \end{eqnarray*}$

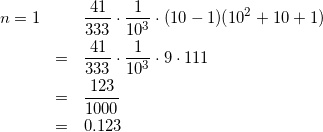
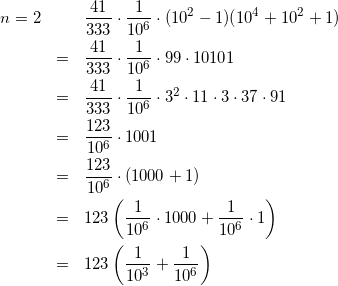
この問題、数１、数２の範囲がうまく融合しているので、どこかの入試問題として出題されててもおかしくないですね。

オンライン指導、生徒受付中！2月3月に指導開始の場合、割引！

神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。

対象学年：中学生、高校生、浪人生
指導科目（高校）：数学、物理、大学受験指導
指導科目（中学）：数学、理科、高校受験指導
指導形態：SkypeまたはZoomによるオンライン指導
指導曜日・時間：要相談
料金：1時間6,000円（税別）→5,000円（2月3月指導開始の方だけ！）
体験指導：60分（ヒアリング含む）

体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

お問い合わせ

回答例

四国の公立高校入試制度まとめ

ニューヨーク大学が医学部の学費を全額免除したらしいよ。

分数の割り算はなぜ逆数をかけるのか？

COMMENT コメントをキャンセル