2016年度版スタンダード数学演習12AB、問題番号358の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だけではわかりにくい部分を数学が苦手な人にもわかるように平易な説明をしてあるので参考にしてみてください。
準備
方針:問題文と(1)〜(3)をよく読んで、どんな図形を書けばいいか予想する。
図形に関する問題はどんな図を書くかによって解きやすさが変わってきます。いきなり解き始めるのではなく、まずはどんな図を書けばいいか手を動かしながら考えてみましょう。
問題文を読むと、(2)で点Cから面OABに垂線CHを引いています。最終的に(3)で体積を求めさせようとしています。これらの情報から面OABを底面、CHを高さとする三角錐を書けばいいのではないかと推測することができます。

直線OHとABの交点をIとしました。これで問題を解く準備ができました。実際に解くときは最初から解きやすい図形を描けない場合も多いと思いますが、そういうときは描き直しながら解き進めましょう。
解説
(1)の回答例
方針:![]() であることから
であることから![]() であることを利用できないかと考える。
であることを利用できないかと考える。
(![]() を利用するためにまずは
を利用するためにまずは![]() を他のベクトルで表せないか考える。)
を他のベクトルで表せないか考える。)
(1) 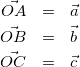
とする。
(2) ![]()
また、
(3) ![]()
点Iは線分ABの中点なので、
(4) ![]()
式(3)、式(4)より、
(5) 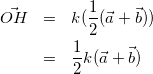
![]() であること、式(2)と式(5)より
であること、式(2)と式(5)より
(6) 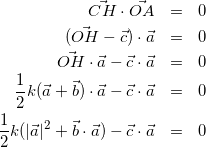
(ここで![]() や
や![]() の値が必要になるので計算します。)
の値が必要になるので計算します。)
(7) 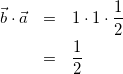
(8) 
式(6)〜(8)より,
(9) 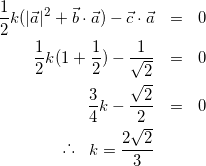
式(5)と式(8)より、
(10) 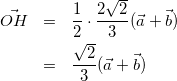
(1)のポイント
(1)のポイントは以下の2点です。
- 「2つのベクトルが垂直 → 内積=0」の利用
- 面に含まれるベクトルの利用
ベクトルの問題で垂直ときたら内積=0を利用するところまではみなさん思いつくと思います。
空間図形の場合、“あるベクトルと垂直な面に含まれるベクトル”も、あるベクトルと垂直になるということを利用することが多いです。
いまの場合はCHと面OABが垂直なので、面OABに含まれるベクトルを利用します。(CHが面OABと垂直であるということは![]() ということでもあります。)
ということでもあります。)
聞かれているのは![]() なので
なので![]() を
を![]() を使って表すことを考えることを思いつけるかどうかですが、実際に解くときは試行錯誤しながら解かなければいけないということも頭に入れておきましょう。
を使って表すことを考えることを思いつけるかどうかですが、実際に解くときは試行錯誤しながら解かなければいけないということも頭に入れておきましょう。
(2)の回答例
方針:![]() を利用する。
を利用する。
(11) 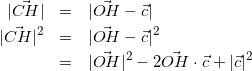
(ここで、![]() や
や![]() の値が必要なので計算します。)
の値が必要なので計算します。)
(12) 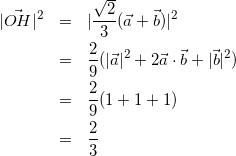
(13) 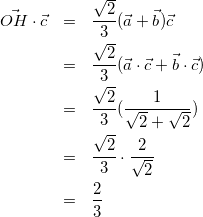
式(11)〜(13)より、
(14) 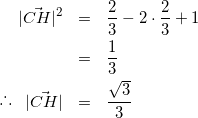
(2)のポイント
ここでのポイントは以下の2点。
- CHの長さは
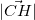 で表すことができる
で表すことができる - すでに
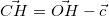 を知っている
を知っている
つまり,![]() を利用すればうまくいきそうだと予想できます。この形をみたら両辺を2乗したくなるはずです(ならない人は演習不足!)。
を利用すればうまくいきそうだと予想できます。この形をみたら両辺を2乗したくなるはずです(ならない人は演習不足!)。
(3)の回答例
方針:錐体の体積の求め方に従って解く。
(面OABを底面、CHを高さとして考えているので体積を求めていく)
(15) 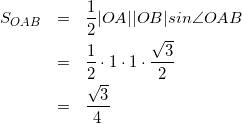
(16) 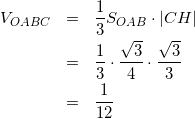
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。


