2016年度版スタンダード数学演習12AB、問題番号335の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だけではわかりにくい部分を数学が苦手な人にもわかるように平易な説明をしてあるので参考にしてみてください。
以下、解説です。
実はこの問題はベクトルの知識は使わず数１Aの知識で解けます。解説通りだと計算が面倒（?）なのでそっちの解法のほうが効率的かもしれないですね。
解説
回答例
ここでは、ベクトルを使わないで解く方法を紹介します。ベクトルでも良いのですが、あえてベクトルで解く必要もないので。
方針：最終的には
のようにチェバ・メネラウスの形に持って行くことを考えます。それに気づくためには図を書いて、色々試して行くと良いと思います。
（まずは問題文を図におこします。）
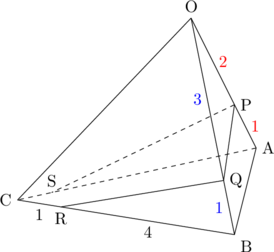
（次にPSとQRを延長します。これは経験値をためないと思いつかないところ。）
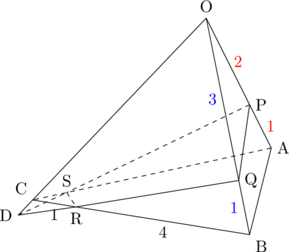
（ここまで来た時に、「を使えそうだな」「ということはあとは
が欲しいな」と思えると良いですね。）
（を使えるかどうか、わかりやすくするために平面を取り出してみましょう。）
（が欲しいので以下の面を取り出して考えましょう。）
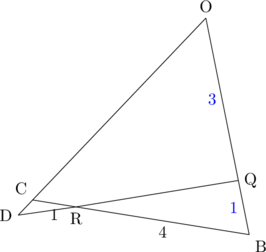
（あとはに代入するだけです。）
(1) 
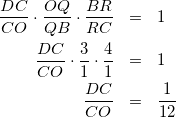
これを面OACを含む面の方で使います。
(2) 
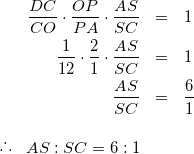
この問題のポイント、アドバイス
この解き方はチェバ・メネラウスが使えそうだなと思いつくかどうかが最大のポイントです。
思いつけるようになるにはどうするかというと、普段から以下の３点について意識して勉強しておくと良いと思います。
- 図を書く
- 図形を拡張する（補助線を引く）
- チェバ・メネラウスの定理の利用
図を書くというのはこの問題に限ったことではないですが、「ひらめかない！」という人の多くは図を書いていません。
また、補助線を引くというのも基本動作ですが、「どう引けば良いのか」は経験値をためるしかないですね。
経験値のため方としては以下のことを頭に入れておくといいでしょう。
チェバ・メネラウスの式において、辺の比が2セットわかっていれば残りの1つの辺の比は求められる。
今の場合は「
を求めたいのでそれ以外の比がわかれば良さそうだ！」と反応できれば良いと思います。
ただし、そう思いついた時点ではほとんどの場合、それが正解ルートかどうかわからない、だから試してみよう！と考えて手を動かすこと、普段からそういう行動を取ることが重要です。
そうすることで、次第に「ひらめき力」がレベルアップしていきます。
この問題はスタンダード数学演習12ABの中ではベクトルに分類されてますが、ベクトルの出題側（早稲田大学）としてはどういう意図だったんでしょうかね。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年：中学生、高校生、浪人生
- 指導科目（高校）：数学、物理、大学受験指導
- 指導科目（中学）：数学、理科、高校受験指導
- 指導形態：SkypeまたはZoomによるオンライン指導
- 指導曜日・時間：要相談
- 料金：1時間6,000円（税別）→5,000円（2月3月指導開始の方だけ！）
- 体験指導：60分（ヒアリング含む）
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。
