スタンダード数学演習12AB-2016

スタンダード数学演習の解説　334・ベクトルの基本　[2016]

  /
2016スタンダード数学演習12AB-アイキャッチ画像

2016年版スタンダード数学演習12AB、問題番号334の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だけではわかりにくい部分を数学が苦手な人にもわかるように平易な説明をしてあるので参考にしてみてください。

(1)の回答例

方針：4\vec{PA}+5\vec{PB}+6\vec{PC}=\vec{0}（①とする。）を\vec{AP}、\vec{AB}、\vec{AC}だけで表すことを考える

（①の式を使うという判断は経験値がないとできませんが、問題文で与えられている式は２つしかないので、両方とも試せば良いですね。）

 

（①の式を踏まえて適当に図を書きましょう。）

Rendered by QuickLaTeX.com

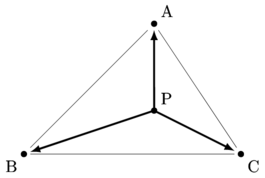
（この時点では点Pの位置はどこでもOKです。三角形ABCの内部になくても問題ありません。①の式の形から点Pは三角形ABCの内部にあることがわかるのですが、なぜなのかは教科書等で調べてみればすぐにわかるはずです。）

 

この図より、

(1)   \begin{eqnarray*} \vec{PB}=\vec{AB}-\vec{AP}\\ \vec{PC}=\vec{AC}-\vec{AP}\\ \end{eqnarray*}

 

よって、

(2)   \begin{eqnarray*} 4\vec{PA}+5\vec{PB}+6\vec{PC}&=&\vec{0} \\ -4\vec{AP}+5(\vec{AB}-\vec{AP})+6(\vec{AC}-\vec{AP})&=&\vec{0} \\ &\vdots& \\ \vec{AP} &=& \frac{1}{3}\vec{AB}+\frac{2}{5}\vec{AC} \end{eqnarray*}

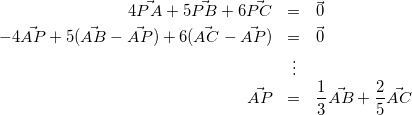
（計算結果からも点Pは三角形ABCの内部にあることがわかりましたね。）

 

(1)のポイント

(1)の最大のポイントは次の１点。

  • ①を式変形すればOKと反応できるかどうか

この解法はよく使うので覚えておきましょう。

式変形するときのポイントは、最終的には\vec{AP}、\vec{AB}、\vec{AC}の3つのベクトルだけで表したいということです。こういうときは仮でいいので図を書いて考えましょう。

最初の段階では、ほとんどの人が「①を式変形すれば解ける！」という確信は持てないはずです。

「とりえあえず式変形してみるか」くらいの気持ちで進めていき、どこかの時点で「あ、これイケる！」となるはずです。

 

\vec{AP}はベクトル方程式を解いてもいいですが、それだと時間がかかります。ここで解説した解法は特別なものではないですが、実際の試験になると忘れがちなのでしっかり整理しておきましょう。

 

(2)の回答例

方針：まずは(1)の結果を踏まえてもう一度図を書いてみるところからスタート

（(1)の結果から点Pが三角形ABCの内部にあることがわかりました。今度は仮の図ではなく、(1)の結果を反映した図を書いてみましょう。）

 

(1)より、

(3)   \begin{eqnarray*} \vec{AP} &=& \frac{1}{3}\vec{AB}+\frac{2}{5}\vec{AC} \\ &=& \frac{5\vec{AB}+6\vec{AC}}{15} \\ &=& \frac{11}{15}\cdot\frac{5\vec{AB}+6\vec{AC}}{11} \end{eqnarray*}

 

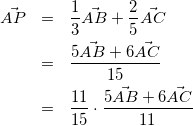
よって点Pは、線分BCを6:5に内分する点をEとするとき、線分AEを11:4に内分する点であるので、以下のような図が得られる。

Rendered by QuickLaTeX.com

 

（これでようやく三角形PABと三角形PBCの面積の比を求める準備ができました。三角形ABCの面積を基準にして考えます。）

 

    \begin{eqnarray*} S_{PAB} &=& \frac{11}{15} S_{ABE} \\ &=& \frac{11}{15}\cdot\frac{6}{11} S_{ABC} \\ &=& \frac{2}{5}S_{ABC} \\ \vspace{5mm} \\ S_{PBC} &=& \frac{4}{15} S_{ABC} \\ \vspace{5mm} \\ \raisebox{.2ex}{.}\raisebox{1.2ex}{.}\raisebox{.2ex}{.} \hspace{3mm} S_{PAB}:S_{PBC}&=&\frac{2}{5}S_{ABC}:\frac{4}{15}S_{ABC} \\ \vspace{3mm} \\ &=&3:2 \\ \end{eqnarray*}

 

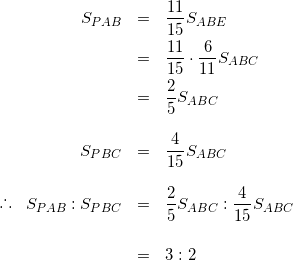
(2)のポイント

(2)のポイントは次の１点。

  • (1)の結果を踏まえて図を書く

①の式の形を見て内分の知識が使えそうだと反応できるかが最大のポイントですね。

①を式変形すれば「BCを6:5に内分する点をEとするとき、点Pは線分AEを11:4に内分する点」ということがわかります。

（＊ここのパートは「BE:EC=t:1-t」のようにおいて\vec{AE}について2つ式を作り係数比較して解く方法もありますが、少々めんどくさいです。興味がある人はやってみてください。）

 

(3)の回答例

方針：(1)、(2)と同じように考える

 

（まずは(2)までの結果をもとにして図を書いてみましょう。）

Rendered by QuickLaTeX.com

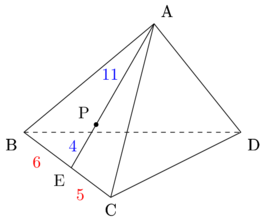
（4\vec{QA}+5\vec{QB}+6\vec{QC}+7\vec{QD}=\vec{0}（②とします。）という条件式から点Qは三角錐ABCDの内部にあることがわかります。）

 

（そこで②の式を(1)と同様に、\vec{AB}、\vec{AC}、\vec{AD}で表していきます。点Qは内部じゃなくてもいいので適当に書いてみてください。）

(4)   \begin{eqnarray*} 4\vec{QA}+5\vec{QB}+6\vec{QC}+7\vec{QD}&=&\vec{0} \\ -4\vec{AQ}+5(\vec{AB}-\vec{AQ})+6(\vec{AC}-\vec{AQ})+7(\vec{AD}-\vec{AQ})&=&\vec{0} \\ \vec{AQ}=\frac{1}{22}(5\vec{AB}+6\vec{AC}+7\vec{AD}) \end{eqnarray*}

 

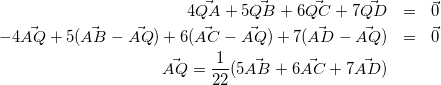
（ここで再びさきほどの解法を利用します。これを思いつくかどうかが素早くとけるかどうかの別れ道です。）

(1)より、

(5)   \begin{eqnarray*} \vec{AP}&=&\frac{11}{15}\cdot\frac{5\vec{AB}+6\vec{AC}}{11} =\frac{11}{15}\vec{AE} \\ \vspace{5mm} \\ \raisebox{.2ex}{.}\raisebox{1.2ex}{.}\raisebox{.2ex}{.} \hspace{3mm} 5\vec{AB}+6\vec{AC} &=& 11\vec{AE} \end{eqnarray*}

 

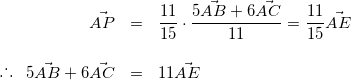
式(5)を式(4)に代入すると、

(6)   \begin{eqnarray*} \vec{AQ}&=&\frac{1}{22}(11\vec{AE}+7\vec{AD}) \\ &=& \frac{18}{22}\cdot\frac{11\vec{AE}+7\vec{AD}}{18} \\ &=& \frac{9}{11}\cdot\frac{11\vec{AE}+7\vec{AD}}{18} \end{eqnarray*}

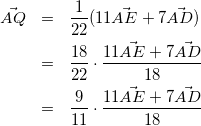
すなわち、線分EDを7:11に内分する点をFとするとき、点Qは線分AFを9:2に内分する点である。これを図で表すと以下のようになる。

 

Rendered by QuickLaTeX.com

 

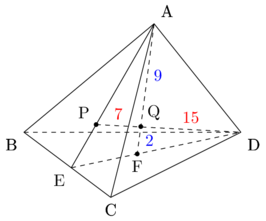
（これで三角錐QABCと三角錐QBCDの体積を比較する準備が整いました。それぞれ三角形ABCと三角形BCDを底面と見て、三角錐ABCDの体積を基準にして考えましょう。）

(7)   \begin{eqnarray*} V_{QABC} = \frac{7}{22}V_{ABCD} \\ \vspace{3mm} \\ V_{QBCD} = \frac{2}{11}V_{ABCD} \\ \vspace{5mm} \\ \raisebox{.2ex}{.}\raisebox{1.2ex}{.}\raisebox{.2ex}{.} \hspace{3mm} V_{QABC}:V_{QBCD}&=&\frac{7}{22}V_{ABCD}:\frac{2}{11}V_{ABCD} \\ \vspace{3mm} \\ &=& 7:4 \end{eqnarray*}

 

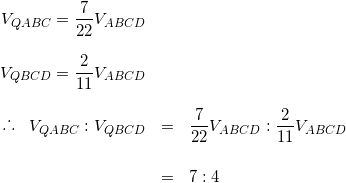
(3)のポイント

(3)のポイント

  • (1)、(2)でやったことを空間図形で同じことをするだけだと反応できるかどうか

 

(2)の結果を踏まえて図を書いたときに、点Qが線分PD上にありそうだと思った人は勘が良いですね。このイメージがあればさきほどの式②をどう式変形していけばいいかなんとなく予想できます。この形はよく見ますからね。ここまできても反応できない場合は演習不足なので、しっかりこの形を頭に叩き込んでおきましょう。

問題A ベクトル スタンダード数学演習
オンライン指導、生徒受付中！2月3月に指導開始の場合、割引！

神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。

  • 対象学年：中学生、高校生、浪人生
  • 指導科目（高校）：数学、物理、大学受験指導
  • 指導科目（中学）：数学、理科、高校受験指導
  • 指導形態：SkypeまたはZoomによるオンライン指導
  • 指導曜日・時間：要相談
  • 料金：1時間6,000円（税別）→5,000円（2月3月指導開始の方だけ！）
  • 体験指導：60分（ヒアリング含む）

 

体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

お問い合わせ

関連記事

COMMENT

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

CAPTCHA