神奈川県公立高校入試で残り1ヶ月で合格するための数学の勉強方法をまとめました。この記事では目標200〜250点の人向けの勉強方法です。ぜひ参考にしてみてください。
ごちゃごちゃとめんどくさい説明を読みたくない人もいると思うので先に超ざっくりとした結論だけ書いておきます。ちゃんとやれば1ヶ月で目標達成できると思います。
超ざっくりと言えば以下の手順で進めればOKです。
- 10分間基礎ドリル 計算、模擬テストで計算をマスターする
- 数学 一問一答問題集、模擬テストで第3問小問集合、第2問(エ)対策
- 15時間完成シリーズ、模擬テストで第4問~第6問の(ア)、第7問の最初の2点をトレーニングする
- 過去問や模擬テストで本番同様のトレーニングをする
- 合格!
*適宜、まとめの復習をやりましょう。
これを読んで具体的な勉強方法がイメージできない人は以下に書いてある内容を読むことをオススメします。早ければ1時間くらいで読み終わります。全体の流れとポイントをおさえた上で勉強した方が圧倒的に効率が良いので、めんどくさがらずに読んでみましょう。
どうしても読むのがめんどくさいと言う方は14.勉強のスケジュールから読んでください。
誰のための記事か
この記事は、
・神奈川県公立高校入試で合計得点200~250点、1科目平均40~50点を目標としてる人
・今までほとんど勉強してないけど、残り1ヶ月でなんとかしたい!という人
・入試で数学40~50欲しいけど現状10~くらいしか取れない人
・現状ほぼ0点だけど、やる気だけはあるって人
・塾に通わず独学する人
・塾に通ってるけど効果がない人
向けです。この中のいくつかが当てはまってればOK。
1ヶ月で合格できるかどうかはあなた次第ですが、頭は良いけど勉強してなかっただけの人ならここに書いてある方法で合格できるはずです。頭悪いけどコツコツやってきた、でも今ひとつ伸びないという人もここに書いてある方法で合格可能性が飛躍的に上がるはずです。
問題は神奈川県のものを扱ってますが、勉強方法の核となる部分は基本的にどの都道府県でも同じなので、他の都道府県の公立高校入試対策でも使えると思います。参考にしてみてください。
前提の学力
残り1ヶ月で1から勉強して合格するための方法を書きましたが、最低限の条件はあります。
条件1
・現状、計算で最低でも9点/24点は取れる
・現状、第3問で4点取れる
条件2
・現状、0点かそれに近い状態だが、ここに書いてある勉強方法をスタートして2~3日で計算ほぼ満点取れるようになった
このどちらかの条件を満たしていれば数学については目標を達成できる可能性が高いです。条件1はある程度勉強してきたけど、本格的に受験勉強はしてない人ですね。条件2は今まで勉強してこなかったけど、実は頭がいい人ですね(ごく稀にそういう人もいます)。
この条件はあくまでも目安なので、この条件に当てはまらないからといって諦めない方が良いです。どんな方であれ、まずはこの記事で書いてある勉強方法をスタートしてみましょう。
勉強時間は70時間しかない!
1ヶ月=30日、1日12時間勉強するとして360時間。5科目を均等に勉強するとして、1科目あたり72時間しかありません。この約70時間の使い方が重要になってきます。何にどのくらいの時間を使うべきかを以下で説明していきます。
入試の問題パターンと配点
まずは入試の問題をチェックしましょう。こちら(平成29年度神奈川県公立高等学校入学者試験問題)で見れます。
毎年だいたい同じ問題パターンなので対策するのは簡単です。言ってみればモンハンで行動パターンがずっと同じモンスターと戦うようなもんです。簡単でしょ?
神奈川県の数学はだいたいこんな感じの構成になってます。
第1問(12点)、計算3点×4問
第2問(17点)、計算4点×3問、図形5点×1問
第3問(21点)、小問集合4点×4点、5点×1問
第4問(関数、15点)、5点×3問
第5問(確率、10点)、5点×2問
第6問(空間図形、15点)、5点×3問
第7問(証明記述、10点)、2点、6点、2点
合計100点満点
最も重要なポイントは、第1問~第3問で「50点もある!」ということです。第1問~第3問は計算や基本事項なので第4問~第7問よりも簡単に解けるようになります。つまり第1問~第3問を重点的に勉強するのが正解ルートです。
さらに第1問~第3問の中でも計算は24点分もあるのでめちゃくちゃお得です。第1問と第2問の計算は例年、中1~中3内容から1問ずつ出題されます。正負の数、文字式、平方根、連立方程式、二次方程式、などは頻出です。
第3問は小問集合で21点分もあります。各単元の計算以外の知識が問われます。変化の割合や変域、資料の整理、1次不等式、整数、平方根の大小、などが出題されやすいです。残り1ヶ月のように時間がない場合は、完璧にするのではなく70~80%をカバーすれば良いと考えておきましょう。そうすれば5問中3問くらいは取れるようになります。
第4問の確率はおおまかな出題パターンは毎年同じです。(ア)は比較的簡単な問題、(イ)はちょいムズ。ここは(ア)だけトレーニングします。(イ)はやるだけ時間の無駄なので捨てましょう。
第5~6問もおおまかな出題パターンは毎年同じです。(ア)は比較的簡単な問題、(イ)はちょいムズ、(ウ)は難問。ここは(ア)を得点できるレベルにします。(イ)と(ウ)は捨てます。
第7問は相似の証明ですが、配点箇所が3つに分かれています。最初の2点分は誰でも取れるのでそこを得点できるレベルにします。
どこで何点取るか
第1問の計算は12点満点を取る
第1問は全て計算です。計算は最もコスパが良いので、満点の12点を必ず取りましょう。ここで失点すると目標達成が難しくなります。
第2問は計算満点を取る
第2問は(ア)〜(エ)の4問構成ですが、なぜか(エ)だけ平面図形です。(ア)〜(ウ)の計算12点分は確実に得点しましょう。第1問と合わせて最悪でも1ミスで抑えられるように勉強しましょう。
第3問は5問中4問(16点)取る
第3問は4点×4問、5点×1問の計21点です。この中で、比較的簡単な(ア)〜(エ)の4点×4問は最低でも取っておきたいところです。ここは出題パターンの種類が多いのでコスパはあまりよくありませんが、難易度自体は高くないので確実に得点したいところです。ここも最悪1ミスで抑えましょう。
第1問〜第3問までで40点/50点を取る
ここまで書いた通り得点できれば、第1問から第3問までで40点取れます。40点取れれば目標の70~80%は達成したことになるので、第1問~第3問はしっかり時間を使うようにしましょう。とは言え、第4問~第7問は得点できるレベルになるまで時間がかかるので、ここまでは素早く勉強を進めたいところです。
第1問と第2問の計算で1ミス、第3問(ア)~(エ)で1ミス、するとそれだけで7~8点の失点になり、目標達成が難しくなります。第3問の得点したい場所でのミスは1つで抑えられるように勉強しましょう。
第4問~第6問の(ア)で10点を取る
第4問~第6問は難しいですが、出題パターンは限られているので対策はしやすいです。大問ごとトレーニング問題集から始めて、予想問題集、過去問でトレーニングすれば(ア)はほぼ解けるようになります。第4問~第6問の(ア)の配点はすべて5点なので、取り切れれば15点分です。
そのうち2問できれば10点取れます。第4問~第6問(ア)は問題設定が第3問までよりも難しいので、勉強するのに時間がかかります。また、正答率も落ちます。そういうイメージで勉強しましょう。
第7問は部分点で2点を取る
第7問は相似の全証明です。多くの人が苦手とする問題ですが、その性質を知っていれば恐れる必要はありません。全証明は例年、以下のような3箇所の配点箇所があります。
「2組の角がそれぞれ等しい」パターン
相似条件1が書かれている(仮定の利用)[2点]
相似条件2が書かれている(仮定の利用)[6点]
相似1,2から「2組の角がそれぞれ等しい」が導かれている[2点]
*どの項目も理由と結論が正しく書かれてないとダメ
「2組の辺の比とその間の角がそれぞれ等しい」、「3組の辺の比がそれぞれ等しい」パターン
相似条件1、2が書かれている(仮定の利用)[2点]
相似条件3が書かれている(自分で考えるとこ)[6点]
相似1,2,3から「2組の辺の比とその間の角がそれぞれ等しい」、「3組の辺の比がそれぞれ等しい」のどちらかが導かれている[2点]
*どの項目も理由と結論が正しく書かれてないとダメ
証明が苦手な人は無理せずに最初の2点を取ることに集中しましょう。証明が得意な人は10点満点を狙いましょう。苦手か得意かすらわからない人はまずは最初の2点を取るための勉強に集中した方がリスクは少なくなります。ここの勉強時間は6時間が目安です。
ここまでで52点分です。
使うテキストの種類と用途
まず、そろえるべきテキストの種類とその用途を説明します。オススメのテキストは後述します。
参考書
わからないところを調べるときに使います。よほどの自信がない限り1冊は持っておきましょう。レベルは3段階くらいに分かれてますが、入試目標が60~70の場合は標準レベルのものを使うと良いと思います。現状の学力があまりにも低い場合は基本レベルのものを使いましょう。
過去問
本番同様のトレーニングをするために使います。基本的に5科目収録されているはずです。6年度分収録されてるもの、英語のリスニングがついてるもの、を1種類でいいので購入しましょう。
模擬試験
これも本番同様のトレーニングをするために使います。過去問だけでは演習量が不足するのでこちらも1種類は持っておきましょう。足りなければ他の種類のものを購入すると良いですね。本番の得点は過去問や模擬試験の演習量に比例して上がっていくので、より合格確率を高めたい人は2種類以上使うのをオススメします。5回分など多めに収録されてるものを購入しましょう。
計算トレーニング用問題集
すでに書いたように、神奈川県の入試は計算だけで24点分あります。ですので計算は毎日のようにやったほうがいいです。特に、本番まで残り1ヶ月だけどこれから勉強スタートする人は、計算力が足りないはずなので必須です。計算は1問もミスれないので、計算OKな人も1種類は購入して毎日トレーニングしましょう。
小問集合対策用問題集
第3問対策用に使います。これがあるのとないのとでは第3問の得点力が大きく変わります。ぜひ1種類は持っておきましょう。
大問ごとのトレーニング用問題集
大問ごとにトレーニングするときに使います。例えば第5問・関数のトレーニングだけしたい場合に使います。学力が足りてない人が過去問や模擬試験だけでトレーニングしてもレベルは上がりません。参考書と本番レベルまでの橋渡しとして使用します。これも小問集合対策用と同様に、あるのとないのとでは得点力に大きな差が出ます。各大問に対応したものを全種類持っておくのをオススメします。
使うテキストの種類はこれだけです。
使うテキスト
次にそれぞれのおすすめテキストを紹介します。
オススメの参考書
高校入試完全攻略3年間の総仕上げ
メリット:入試で使う知識をまとめてあるので効率が良いです。
デメリット:その分、不足する知識も出てきたり、解説が弱い場合もある。
*新版が出てる可能性があるので本屋で確認したほうが良いです。
やさしい中学数学
メリット:説明がていねいでわかりやすいので学力が低い人向けです。
デメリット:説明がていねいな分、分厚い。なので、知りたいことを微妙に調べにくい。
Gakkenニューコース
メリット:標準レベルの参考書。
デメリット:装丁が独特。学年毎に購入する必要あり(3年分がまとまってるのも売ってるかも)。
学力低めの人は、「高校入試完全攻略3年間の総仕上げ」か「やさしい中学数学」
学力普通or高めの人は、「高校入試完全攻略3年間の総仕上げ」か「チャート」
をオススメします。また教科書ガイドのような参考書もありです。ここで紹介したものを本屋で手にとってみてデザインが気に入ったやつを使いましょう。
塾用の参考書
番外編として塾用のテキストも紹介しておきます。塾用で独学するときに使いやすいのは「Iワーク」ですね。多くの個別指導塾でIワークが使われていると思います。「新中学問題集」はもう少し上のレベル向けです。塾用の参考書は基本的には市販されてません。
過去問
過去問は以下のどれかを使えばOK。
(2024/07/26 15:57:22時点 Amazon調べ-詳細)
(2024/07/27 13:52:22時点 Amazon調べ-詳細)
模擬試験
過去問だけだと演習量が足りないと感じる場合は市販の模擬試験も使うと良いと思います。
このあたりがオススメです。本屋にも置かれているのですぐに見つかると思います。
また、神奈川県高校入試の模試といえば伸学工房の全県模試ですが、全県模試はこちらで購入することができます。上記の模試問題集か全県模試のどちらか一方は持っておくのをオススメします。また、同じく伸学工房で購入できる「プレテスト」もオススメです。
計算トレーニング用問題集
こんな小学生みたいのでいいのか、と思うかもしれませんが、これがベストです。これの中1〜中3のやつをそろえましょう。問題量が多くて基本からトレーニングできることがその理由です。
一般的な問題集は1学年の内容が1冊に入っていて計算演習が少ないのでダメです。計算は計算のみ収録されているこういうタイプが最強です。
他にも以下のような類似のものもあるので、上記だけでは足りない場合は追加で使いましょう。
どれも似たような感じですが、下のものほど1回が短時間で終わります。
小問集合対策用問題集
小問集合対策用の問題集は種類があまりないですが、これがオススメです。他の科目のものもあるのでぜひ活用しましょう。これも本屋にあるので探してみてください。第2問(エ)、第3問全部のトレーニングができます。さらに他の大問の基礎作りにもなります。
大問ごとのトレーニング用問題集
(2024/07/27 13:48:01時点 Amazon調べ-詳細)
大問ごとのトレーニング用もあまり種類がないですが、これがオススメです。関数など他の大問用もあります。
演習量が足りない場合は追加で以下のものを購入すると良いでしょう。
これ以外にも”塾技100″というのもありますが、これは少しレベルが高い人向けなのでオススメしません。
塾用の教材
計算トレーニング用、過去問、模擬試験の他に、塾用の教材である「県トレ」と「GetThrough」があれば数学の対策はほぼ完璧です。この2つは小問集合対策、大問対策に最適なので、持ってる人はぜひ有効利用しましょう。ただし、必要なレベルを超える問題をやらないようにしましょう。
超効率勉強法その1
基本的な勉強方法は学力に応じて2パターンに分かれます。
学力低い人
- 参考書で基本の解き方を確認する
- 問題集で演習する
- 模擬試験で演習する
- 過去問で演習する
学力高い人は上記1をカットしてもOK。
最短距離で本番レベルを解けるようにするにはこれが最適です。あとは適切なテキストさえあればなんとかなります。
ここで1つ重要なことがあります。それは過去問は上記スケジュールのパート6まで温存しておくことです。一度解いたことがある問題を解いても、本番同様のトレーニングにならないので最後まで取っておきましょう。なんですが、それまでに本番レベルのトレーニングはしておかないとレベルが上がらりません。そのために模擬試験を使います。
超効率勉強法その2
これは言うまでもないと思いますが、テキストには基本的に書き込まないようにしましょう。復習するときに同じ問題を何回も解くことになるので、書き込むとそれができなくなります。
これも言うまでもなさそうですが、ノート作りは不要です。というかやってはダメです。時間が限られているのでノートを作っている時間はありません。そんな時間があるなら問題を解きまくりましょう。
基本テクニックとしてもう1つ。寝る前15~20分でいいので、その日勉強したことに目を通しましょう。これだけで記憶への定着度が大幅に上がります。数学だったら問題を見て、解法を思い浮かべるだけでOKです。
超効率勉強法その3
ここ超重要なのでちゃんと読んで欲しいところです。これを読んで実行しようとしてる人はそもそもあまり勉強してない人なので、いきなり問題を解くのは難しいと思います。過去問なんてなおさらです。ですので、以下の手順に従って進めましょう。
- 問題を読む
- 1の問題の解説を熟読し解法を理解する
- すぐに、同じ問題を何も見ずに解く
- 丸つけ&再理解
- 類題演習
- 丸つけ&解法の確信を得る
計算トレーニング以外はこの方法が有効です。例えば、第4問・確率の勉強をスタートした直後に、参考書の問題と解き方を熟読し上記の手順を追えば、最速で入試問題に対応できます。
ポイントは最初の1と2ですね。いきなりですが、問題と解説を熟読しましょう。これによって最短距離で入試の問題の解き方が身につきます。
3も重要ポイントです。1、2の問題を何も見ずにもう一度解いてください。ここで重要なのは、丸暗記するのではなく、どうしてその解き方をするのか、その公式を使うのか、その計算をするのか、など問題を解くときのポイントをしっかり考えながら解くことです。そうしないとただ覚えるだけになってしまい、すぐに解けなくなります。また、全く同じ問題しか解けない状態になってしまい、本番で得点しにくくなります。
5~6については、これで解ける!という確信を得るまで類題演習を繰り返してください。ただし勉強時間は守らなければいけないのである程度で切り上げて次の問題に移りましょう。
この方法は邪道ですが、時間がない場合は有効です。高校受験程度の問題ならこれでも十分解けるようになります。ただし、すぐに失われるので長期的にはほとんど意味がないです。この点は理解しておいてください。
超効率勉強法その4
入試の問題は問題パターンがだいたい決まっているので、そのパターン毎にトレーニングすると効率がいいです。自分の学力に応じて一度にトレーニングするパターンの数を変えましょう。
例えば、入試の計算問題は以下のパターンがあります。
- 中1正負の数
- 中1文字式
- 中1方程式
- 中2文字式
- 中2連立方程式
- 中3展開
- 中3因数分解
- 中3二次方程式
- 中3平方根
このうち7種類程度が出題されます。
- 学力が低い人は1つずつトレーニングしましょう。実際の手順は以下のようになります。ここでは例として”10分間基礎ドリル 計算”を使うことにします。模擬試験問題集は任意のものとします。
- 10分間基礎ドリルで正負の数をトレーニングする
- 「これで解けるぞ!」という確信が持てたら一旦ストップする
- 模擬試験の計算・正負の数だけ1年度分解く
- 丸つけ、解説読む
- 1〜4を繰り返す
- 模擬試験の計算・正負の数だけを全部解く
1〜4は、正負の数の計算のルールを本当に理解したか確認する部分です。5は強化するための部分です。6は最終チェックの部分です。
学力が高い人はいくつかの問題パターンをまとめて上記と同じことをすると良いでしょう。
この勉強方法は他の大問でも同じです。最短距離で入試数学に対応するにはこの方法がベストです。いまいち理解できないまま時間だけが過ぎていくというリスクがありますが、そういう人はそもそも1ヶ月では無理な人なのであきらめましょう。
超効率勉強法その5
まず、問題を解いたら結果に応じて問題の横に◯、△、×をつけていきましょう。この印で復習すべき問題を管理します。◯は解けた問題、△は解き方は合ってたけど、ケアレスミス。×は解き方が合ってなかったとかそもそもわからなかった問題。
ただし、計算問題だけは△も×として扱いましょう。計算は結果が間違ってたらアウトですからね。厳しくいきましょう。
勉強スケジュールのところには2種類の復習が書いてあります。1つは「前日の復習」です。もう1つは「総復習」です。
前日の復習で復習する問題は「前日の問題演習のときに解けなかった問題(×がついてる問題)」です。誰でもわかると思いますが、解けなかった問題は優先度が高いです。複数ある場合がほとんどだと思いますが、その場合は、その中でもより基本的な問題を優先しましょう。15分で、丸つけ、解説読む、まで終わるようにしましょう。
総復習では、それまでに勉強した問題パターンをできる限り復習します。最初に勉強してから数日経っているので忘れている可能性もありますし、まだまだ精度が低いからです。まずは×だった問題から復習し、時間に余裕があれば△、次に◯の問題も復習しましょう。
総復習のときに効率を上げる方法がもう1つあります。それは「パッと見でOKかどうか判断する」という方法です。◯がついていたとしても忘れている場合もあります。全ての問題に目を通して、パッと見で「これは100%OKだな」と確信を持てる問題は飛ばし、そうでない問題は◯がついていても復習しましょう。こうすることで、抜けを防止できます。
勉強スケジュール
入試目標が40~50点の場合、実際の勉強はこんな感じで進めます。
- 第1問、第2問の計算対策
- 第3問小問集合対策、第2問(エ)対策
- 第4問~第6問の(ア)対策
- 第7問の最初の2点対策
- 本番同様のトレーニング
これを30日間でギュッと詰め込みます。そうとうハードですが頑張りましょう。たった30日頑張って、希望の高校で3年間過ごすか、あまり行きたくない高校で過ごすかが決まる、と思えば頑張れるはず!
無駄なことをしている時間はないので30日間のスケジュールを予め決めてそれ通りに勉強を進めましょう。
パート1(合計17.5時間)
1日目:計算(2.5時間)
2日目:前日の復習、計算(30分、2時間)
3日目:1~2日目の総復習(2.5時間)
4日目:計算(2.5時間)
5日目:前日の復習、計算(30分、2時間)
6日目:前日の復習、計算(30分、2時間)
7日目:1~6日目の総復習(2.5時間)
*ここまでで24点分
パート2(10時間、合計27.5時間)
8日目:計算、前日の復習、第3問・小問集合(15分、15分、2時間)
9日目:計算、前日の復習、第3問・小問集合(15分、15分、2時間)
10日目:計算、前日の復習、第3問・小問集合(15分、15分、2時間)
11日目:8~10日目までの総復習(2.5時間)
*ここまでで32点分
パート3(8.5時間、合計36時間)
12日目:計算、前日の復習、第5問・確率(ア)(15分、15分、2.5時間)
13日目:計算、前日の復習、第5問・確率(ア)(15分、15分、2.5時間)
14日目:12~14日目までの総復習(2.5時間)
パート4(8.5時間、合計44.5時間)
15日目:計算、前日の復習、第4問・関数(ア)(15分、15分、2.5時間)
16日目:計算、前日の復習、第4問・関数(ア)(15分、15分、2.5時間)
17日目:16~18日目までの総復習(2.5時間)
パート5(8.5時間、合計53時間)
18日目:計算、前日の復習、第6問・空間図形(ア)(15分、15分、2.5時間)
19日目:計算、前日の復習、第6問・空間図形(ア)(15分、15分、2.5時間)
20日目:20~22日目までの総復習(2.5時間)
パート6(6時間、合計59時間)
21日目:計算、前日の復習、第7問・証明の2点分(15分、15分、2時間)
22日目:計算、前日の復習、第7問・証明の2点分(15分、15分、2時間)
23日目:24~25日目までの総復習(2時間)
*ここまでで49点分
パート7(6.5時間、合計65.5時間)
24日目:計算、第3問・小問集合(15分、2時間)
25日目:計算、第3問・小問集合(15分、2時間)
26日目:24~25日目までの総復習(2時間)
*ここまでで40点分
パート8(8時間、合計73.5時間)
27日目:本番同様のトレーニング、結果に応じた復習(2時間)
28日目:本番同様のトレーニング、結果に応じた復習(2時間)
29日目:本番同様のトレーニング、結果に応じた復習(2時間)
30日目:本番同様のトレーニング、結果に応じた復習(2時間)
実際の勉強手順
上記の計算トレーニング方法と重複する部分もありますが改めて書いていきます。わかりやすくするために勉強スケジュールに合わせて説明します。
パート1の勉強方法
平成29年度の計算部分はこんな感じです。

勉強の手順は以下の通りです。
- 模擬試験1回分の計算部分だけ解いて丸つけ、解説読む(実力チェック)
- わからなかった問題パターンだけ「10分間基礎ドリル 計算」で1パターンだけ(例えば正負の数だけ)トレーニングする
- 2のパターンを模擬試験でもう一回分解いて丸つけ、解説読む
- 2〜3を繰り返す
- 模擬試験or過去問の計算部分だけ2~3回分解く
基本はこれだけです。超効率勉強法その4のやり方でやるようにしましょう。ポイントは問題パターン毎にトレーニングすることです。
これまであまり勉強したことがない人は複数の問題パターンを同時にやると混乱するので、1つの問題パターンずつ確実に身につけていきましょう。
普通は”10分間基礎ドリル 計算”で一通り勉強してから模擬試験で実力チェックしますが、それだと時間がかかりすぎます。リスクはありますが、このやり方なら1ヶ月で入試の計算問題に対応できるようになります。早い人は一週間もあればイケます。
解説を読んでも理解できない場合は上述の参考書で調べましょう。
4は「これでこのパターンはOK!」と自信が持てるようになるまで繰り返しましょう。OKなら次の問題パターンへ進みましょう。これを繰り返し、全ての計算パターンをマスターしましょう。計算だけで24点分あるので、これだけで目標の50%くらいの点数になります!
その後、5で最終チェックをしましょう。5で合計1ミスくらいであれば次のパートに進んでもOKです。それ未満であれば弱点パターンをトレーニングし直してから次の工程に進みましょう。
計算問題の全体像が掴めたら、パート2以降は毎日15分ずつ”10分間基礎ドリル 計算”でトレーニングしましょう。弱点パターンから優先的にやるようにしましょう。たまに、模擬試験や過去問の計算部分だけを1回分(1年度分)解くなどするとより効果が高まります。
パート1の3日目と7日目に総復習をしましょう。
多くの人は一度解けるようになるとその後もずっと解けると思い込みます。これが本番で「ああ、これやったんだけどなあ」となる原因です。なので、こまめに復習をはさむのが正解です。
全ての問題をやっている時間はないので、上述の勉強法の通り、まずは×が付いている問題を優先してやりましょう。前日の復習をして複数回解いてある問題には印が2個以上ついてるものもあると思います。その場合は×が多い問題から優先的に復習するようにしましょう。
復習するときはいきなり問題を解きましょう。それで解けるのであれば一応は合格です。この総復習においても解いた結果に応じて◯、△、×をつけていきましょう。
パート1はこれで終わりです。
もし、このスケジュールで終わらない場合どうするかについてですが、計算は最もコスパがいいところなので、8日目、9日目にズレても良いので最優先でマスターしましょう。その場合は、以降のリスケジュールをしましょう。
パート2の勉強方法
パート2は第3問の小問集合対策です。以下の画像は平成29年度の問題です。


すでに述べた通り第3問の対策は時間がかかります。このパート1では目標の16点中8点取れるようになればOKだと思って勉強しましょう。
また、下記の問題集を使えば第2問(エ)平面図形のトレーニングもできるので余裕があればやっておきましょう。
- 過去問から、1問だけ問題パターンを選び解説を読む
- すぐに1で選んだ問題をもう一度解いてみる
- 「数学一問一答問題集」で1と同じ問題パターンをトレーニング
- 模擬試験で1、2と同じパターンの問題だけトレーニング
- そのパターンが解けるようになったら1に戻って次の問題パターンを選ぶ
- 1~5を繰り返す
基本はこれだけです。第3問はどのパターンが出題されるか予想できないので、まずは過去に出題されたパターンを1つずつできるようにするのが最も効率が良いです。これができれば8点は取れるようになるはずです。
パート7でもう一度、第3問小問集合のトレーニングをするのでパート2では8点分でOKと考えましょう。
過去問や”数学一問一答問題集”、および模擬試験の解説は基本中の基本部分は省かれていることもあります。理解できない場合は上述の参考書で調べましょう。
おそらく、ほとんどの人はこの時間内に過去問6年度分に載ってる全てのパターンを終えることができないと思いますが、パート7で再び強化するのでOKです。また、”数学一問一答問題集”に載っている全てのパターンをやっている時間はないので、過去問の傾向にない問題はやらずに保留しておきましょう。
ここで1つ注意があります。数学の問題は2016年度(2017年2月試験)で新たに第3問・小問集合が登場したんですが、それ以前は同様の問題パターンは第2問で出題されています。なので、1で問題パターンを選ぶときは気をつけましょう。
パート3の勉強方法
パート3は第5問・確率(ア)の対策です。なぜ第4問の関数ではなく、第5問の確率からやるかと言うと、確率の(ア)は比較的難易度が低く得点しやすいからです。
ここで1つ注意があります。第4問〜第6問の(ア)は全部で3問ありますが、そのうち2問取れれば万歳なので無理にこれら全ての(ア)対策をしようと思わなくてもOKです。
例えばパート3で確率の(ア)を勉強していて予定していた時間が経過した時、もし、もう少しでコツが掴めそうであれば続けて勉強するようにしましょう。
あくまでもパート3~パート5の期間内に、第4問〜第6問の(ア)のうち2問できるようにすればOKです。
しかし、第4問〜第6問の(ア)は一通り触れておくようにしましょう。この中でまったく対策しない問題パターンがあるのはかなりリスクが高いです。
以下の手順に沿って進めましょう。
- 過去問の第5問・確率(ア)だけを見て、解説を熟読する。
- 「高校入試 10日でできるシリーズ」で(ア)レベルまでを勉強する。
- 模擬試験で第5問・確率(ア)だけトレーニング
- 過去問2~3年度分を解いて実力チェック
基本的な知識が不足している場合は上述の参考書で調べながら進めましょう。参考書にある問題も演習として十分使えるので、どんどん活用していきましょう。
普通は2あたりからスタートすると思いますが、どんな感じで出題されるかを知った状態で勉強した方が圧倒的に効率が良いです。初めて行く場所に、目的地付近の画像や動画を見てから行くと目的地に着きやすくなるのと同じです。しかもこの1自体はそこまで時間がかからないのも重要な点です。1~3年度分に目を通せば十分ですね。
2で使う”高校入試 10日でできるシリーズ”を使えば(ア)を解くための知識を身につけることができますが、それだけでは本番での得点力に不安が残ります。1で実際の入試問題を見たらわかりますが、確率の問題はゲームのルールを把握するのが難しいです。(イ)レベルまでやると時間がかかるのでうまく問題選定しましょう。
なので、模擬試験で実際の入試レベルに対応できるようにトレーニングします。この時点で模擬試験は全ての回の(ア)を解いてしまってOKです。慣れてくれば問題を読んですぐに、どの知識を使えば解けるかわかるようになります。
4で過去問を2~3年度分使う理由は解法への自信を持つためと、本番同様のトレーニングのためにとっておくためです。
確率は基本的に「確率=今考えている事象の場合の数/全ての場合の数」で求められます。例えば平成29年度の問題(下記画像参照)だと、「全ての石の白の面が上となる」が今考えている事象になります。具体的な回答は省きます。

パート3では(ア)だけ勉強しましょう。(ア)だけです。この時点で(イ)に手を出すと時間が足りなくなります。
パート3の最後に総復習するのを忘れずに。
パート4の勉強方法
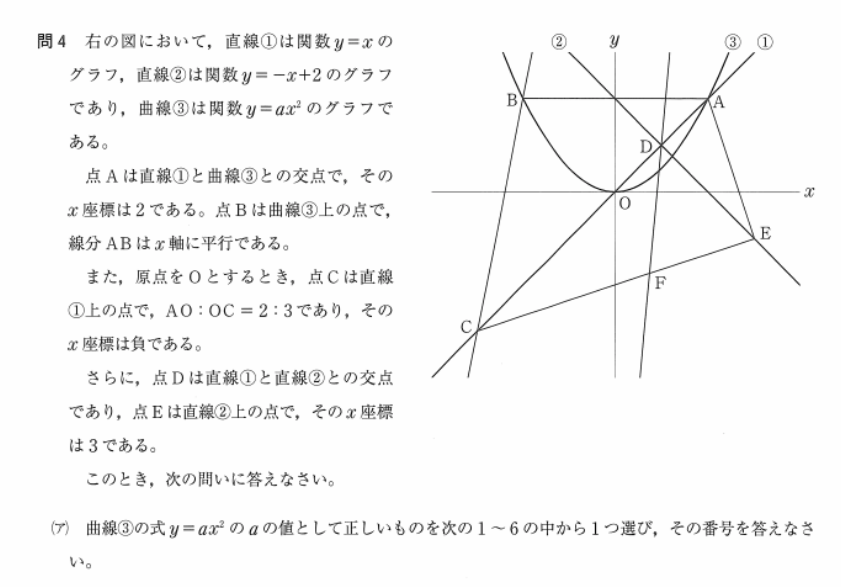
パート4は第4問・関数です。関数は得手不得手が別れるところですが苦手でも(ア)だけは得点しなければいけません。基本的にはパート3と同じやり方でOKです。一応手順を示しておきます。
- 過去問の第4問・関数(ア)だけを見て、解説を熟読する。
- 「15時間完成シリーズ」で(ア)レベルまでを勉強する。
- 模擬試験で第4問・関数(ア)だけトレーニング
- 過去問2~3年度分を解いて実力チェック
パート4の最後にしっかり総復習しましょう。
パート5の勉強方法
パート5は第6問・空間図形です。ここもパート3やパート4と同じです。一応手順を示しておきます。
- 過去問の第6問・空間図形(ア)だけを見て、解説を熟読する。
- 「15時間完成シリーズ」で(ア)レベルまでを勉強する。
- 模擬試験で第6問・空間図形(ア)だけトレーニング
- 過去問2~3年度分を解いて実力チェック
パート5の最後に総復習しましょう。
パート6の勉強方法
パート6は第7問・相似の証明です。ここもパート3〜5までと同じです。2点分なのでそこまで時間をかけないようにしましょう。一応手順を示しておきます。
- 過去問の第7問を見て、解説を熟読する。
- 「15時間完成シリーズ」で最初の2点レベルまでを勉強する。
- 模擬試験で第6問・空間図形(ア)だけトレーニング
- 過去問2~3年度分を解いて実力チェック
証明の配点箇所をここでもう一度確認しておきましょう。

パート6の最後に総復習しましょう。
パート7の勉強方法
パート7は第3問・小問集合の強化です。第3問は第4問〜第6問と比べて簡単な問題が多いので、優先的に得点したいところです。
ここでの勉強方法はパート2と基本的には同じです。パート2で勉強した中でわかっている弱点パターンの強化やまだ触れてないパターンのトレーニングをしましょう。
パート8の勉強方法
パート8は本番同様のトレーニングです。実際の手順は以下の通りです。
- 過去問1年度分を解く
- 丸つけ、解説熟読
- 復習、類題演習
- 1~3を繰り返す
1では本番と同じ時間で解くようにしましょう。また、わからない問題でも適当に書くようにしましょう。第3問~第6問は選択式なので、運が良ければ1つくらい当たるかもしれません。
できれば1は他の科目も合わせて、本番同様のタイムスケジュールで解く方がいいです。その方が本番で慌てなくなります。
3の類題演習は実はいまいち解き方を理解できてない問題パターンだけやるようにしましょう。これまで解いたことがある問題を解き直してみるのもありですが、解いたことがない問題の中で類題があればそっちを優先的に解くようにしましょう。過去問を解いて、間違った問題の解説を読み、その問題の初見類題を解ければ一応はOKですからね。
あとは時間の許す限り1~3を繰り返しましょう。過去問を全てやりつくしたら模擬試験を使いましょう。これもすでに解いたことがあるものよりも解いたことのない回を優先しましょう。全てやり尽くしている場合は、新たに他の模擬試験を購入するのもありです。
この勉強方法のリスク
この勉強方法の最大のリスクは入試の問題パターンの変化に対応できないことです。大問1つが丸々他の問題パターンに変わることも十分考えられます。
例えば、第4問の関数がいろいろな関数に変わることは十分考えられます。でも、ここに書いてある方法は限られた時間内でできるベストな方法です。時間に余裕があれば体系的に学んで行くことでそのリスクを軽減できるんですけどね。
もう1つリスク(というかしょうがないこと)があります。本文の中で何回か書いてますが、もともと頭の悪い人は残念ながらこの方法を持ってしても目標を達成することができない可能性が高いです。
さいごに
これまで10年以上、数百人に個別指導してきた経験を凝縮してこの記事にしました。受験生の方が実行しやすいように書いたつもりです。テキストの解説を読んで理解できるレベルの人じゃないと、1ヶ月ではそもそも目標達成できない、という前提のもとで書きました。
ですので、各問題、例えば「確率はこういう風に考えると解けるようになるよ」のような講義的な内容は省略しました。それをやるとこの文量では終わりませんし、繰り返しになりますが、そもそもそれが必要な人は、残り1ヶ月で、しかも独学でこの目標を達成するのは難しいでしょう。
こういうHowToものを書くときは「誰でもできる」ような内容で書くのが一般的かもしれません。それだけに今までこのような記事を書くのを避けてきましたが、今回、思い切って書くことにしました。ごく少数かもしれませんが、これを読んで目標を達成できる人がいたら嬉しいです。
賢い人は気づくかもしれませんが、時間を増やしてここに書いてある勉強方法をすればより確実に目標を達成できるようになりますし、地頭が悪い人でも目標を達成できるようになります。確実に合格したければ余裕を持って勉強するようにしましょう。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。


















