因数分解の公式の導出方法（3乗公式、4乗公式まで）

中３とか高1で因数分解の公式（乗法公式）覚えさせられると思いますが、今回はその導出方法（証明）を紹介します。以外と知らない人が多いので、ぜひチェックしてみてください。あと、それを利用したちょいムズ因数分解の解き方も解説します。

因数分解の公式（乗法公式）

中3で習う公式はこの3つ。

$\begin{eqnarray*} a^2 \pm 2ab+b^2=(a \pm b)^2\\ a^2-b^2=(a+b)(a-b) \end{eqnarray*}$

なぜこうなるのか、という説明として「右辺を展開すればもとに戻る」と教わることがほとんどだと思いますが、この公式の導出についてはあまり教わらないっぽいので、その導出方法を解説します。

中３で習う因数分解の公式の導出方法

導出は意外と簡単で、2abを分割して考えます。

$\begin{eqnarray*} a^2+2ab+b^2&=&a^2+ab+ab+b^2\\ &=&a(a+b)+b(a+b)\\ &=&(a+b)(a+b)\\ &=&(a+b)^2 \end{eqnarray*}$

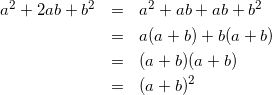
もう一方は、abと-abを足して考えるとうまくいきます。

$\begin{eqnarray*} a^2-b^2&=&a^2+ab-ab-b^2\\ &=&a(a+b)-b(a+b)\\ &=&(a+b)(a-b)\\ \end{eqnarray*}$

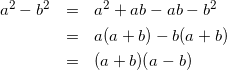
これなら、「共通因数でくくる」という最も基本的な知識だけで導出することができます。言われてみれば簡単ですね。「どうしてこうなるんだろう？」という疑問を大切にしている人は、自力で到達できるやつですね。

３乗公式の導出

実は高校（数１）でやる3乗公式も同じように導出できます。

$\begin{eqnarray*} &&a^3+3a^2b+3ab^2+b^3\\ &=&a^3+a^2b+2a^2b+2a^2b+ab^2+b^3\\ &=&a^2(a+b)+2ab(a+b)+b^2(a+b)\\ &=&(a+b)(a^2+2ab+b^2)\\ &=&(a+b)(a+b)^2\\ &=&(a+b)^3 \end{eqnarray*}$

$\begin{eqnarray*} &&a^3+b^3\\ &=&a^3+a^2b-ab^2+b^3\\ &=&a^2(a+b)-b(a^2-b^2)\\ &=&a^2(a+b)-b(a+b)(a-b)\\ &=&(a+b)\{a^2-b(a-b)\}\\ &=&(a+b)(a^2-ab+b^2) \end{eqnarray*}$

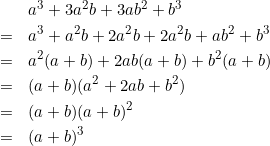
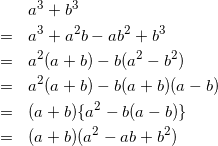
±の組み合わせが異なるやつも同様にできます。

4乗公式？

上記の導出で使ったテクニックは２つ。

項を分割する
項を追加する

実は、これ高校内容の因数分解で使うテクニックだったりします。特に②は。

以下で、①を使って解く問題を紹介します。

$\begin{eqnarray*} a^4+2a^3+2a^2+2a+1\\ \end{eqnarray*}$

これを因数分解するわけですが、やったことないと難しい。でも、上記の①のテクニックを知っていれば解けます。

$\begin{eqnarray*} &&a^4+2a^3+2a^2+2a+1\\ &=&a^4+ a^3+a^3+a^2+a^2+a+a+1\\ &=&a^3(a+1)+a^2(a+1)+a(a+1)+(a+1)\\ &=&(a+1)(a^3+a^2+a+1)\\ &=&(a+1)\{a^2(a+1)+(a+1)\}\\ &=&(a+1)(a+1)(a^2+1)\\ &=&(a+1)^2(a^2+1) \end{eqnarray*}$

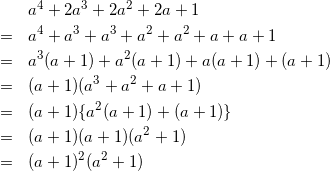
もう１つ。

$\begin{eqnarray*} &&a^4+4a^3b+6a^2b^2+4ab^3+b^4\\ &=&a^4+4ba^3+6b^2a^2+4b^3a+b^4\\ &=&a^4+ba^3+3ba^3+3b^2a^2+3ba^3+ba^3+b^4\\ &=&a^3(a+b)+3a^2b(a+b)+3ab^2(a+b)+b^3(a+b)\\ &=&(a+b)(a^3+3a^2b+3ab^2+b^3)\\ &=&(a+b)(a+b)^3\\ &=&(a+b)^4 \end{eqnarray*}$

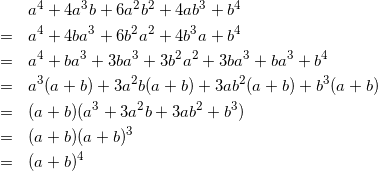
これは４乗公式的な感じですね。これ、実は高校内容の二項定理にも関係するんですよね。こんな感じで数学は次へと繋がってるとわかると面白いですね。

どちらも基本的なテクニックを知っていれば解ける問題なので、上位の大学入試で出題されてもおかしくない問題かも。

オンライン指導、生徒受付中！2月3月に指導開始の場合、割引！

神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。

対象学年：中学生、高校生、浪人生
指導科目（高校）：数学、物理、大学受験指導
指導科目（中学）：数学、理科、高校受験指導
指導形態：SkypeまたはZoomによるオンライン指導
指導曜日・時間：要相談
料金：1時間6,000円（税別）→5,000円（2月3月指導開始の方だけ！）
体験指導：60分（ヒアリング含む）

体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

お問い合わせ

因数分解の公式の導出方法（3乗公式、4乗公式まで）

因数分解の公式（乗法公式）

中３で習う因数分解の公式の導出方法

３乗公式の導出

4乗公式？

POSTED COMMENT

COMMENT コメントをキャンセル

因数分解の公式（乗法公式）

中３で習う因数分解の公式の導出方法

３乗公式の導出

4乗公式？

世界の大学 学術ランキング（ARWU）2018

ニューヨーク大学が医学部の学費を全額免除したらしいよ。

頌栄女子学院の学費、偏差値、入試情報、進学実績まとめ

POSTED COMMENT

COMMENT コメントをキャンセル

世界の大学　学術ランキング（ARWU）2018