ラングレーの問題の解説｜オンライン講師ブログ

今回はラングレーの問題の解説です。この問題は1922年にE・M・ラングレーが発表した平面幾何の難問らしいです。wikiには方針だけ書いてあって細かい解き方が書かれてなかったので、メモもかねて解き方を残しておきます。

ラングレーの問題

まずは問題。

Rendered by QuickLaTeX.com

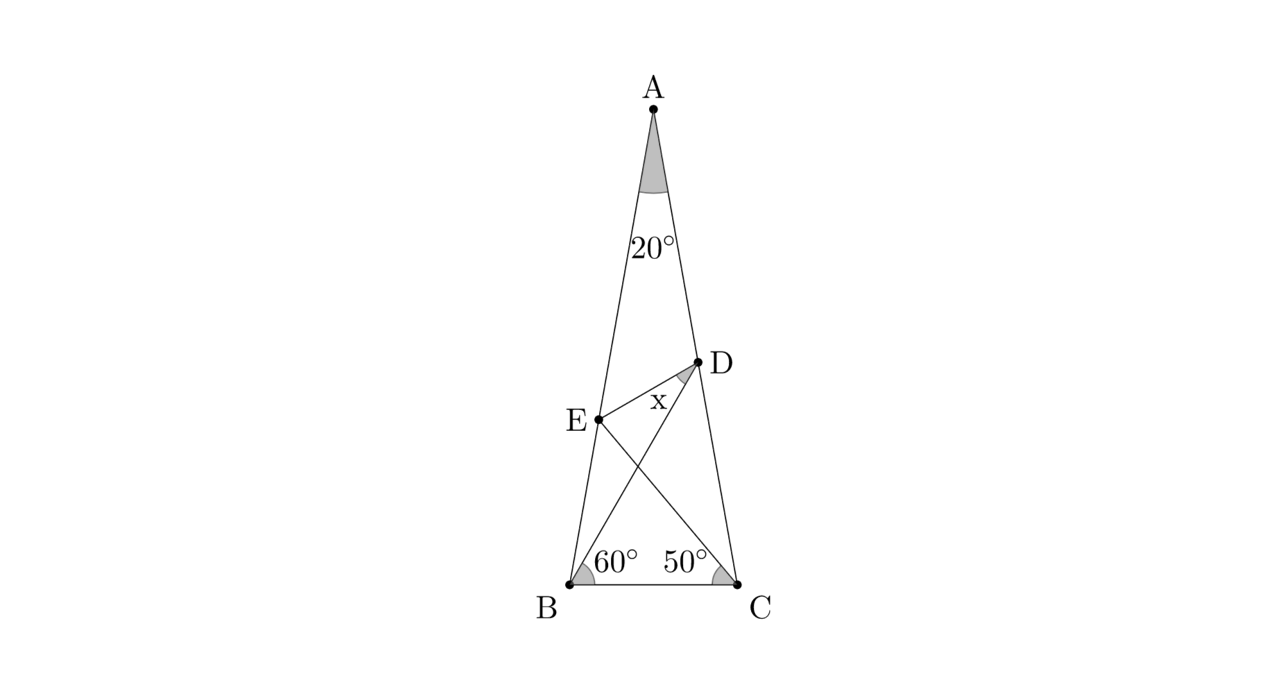
上記の図形においてAB=ACのとき、xを求めよ。

いたってシンプルな問題です。

私は1時間考えても解けなかったので、しょうがなくwikiの方針をチェックしました。

AB上に BD=BF となる点Fをとり、AD=AG となる点GをDFの延長線上にとる。△AGF≡△DBC を示し、FD=FE を示す。

とりあえずこれ通りにやってみました。

Rendered by QuickLaTeX.com

△ABCは二等辺三角形なので、 $\angle ABD = 20^{\circ}$ 、 $\angle ACE = 30^{\circ}$ 。

△BDFは二等辺三角形なので、 $\angle BDF = \angle BFD = 80^{\circ}$ 。

△ABDは二等辺三角形なので、 $\angle ADB=140^{\circ}$ 。また $\angle ADG = \angle ADB - \angle BDF = 140^{\circ} - 80^{\circ} = 60^{\circ}$ 、AD=BD（①）。

AD=AGより△ADGは二等辺三角形なので、 $\angle AGD = 60^{\circ}$ 。よって、△ADGは正三角形。したがってAD=AG=DG（②）。

①②より、AD=AG=DG=BF（③）。

△AFGと△DCBにおいて、一辺の長さとその両端の角がそれぞれ等しいので△AFG≡△DCB。よって、FG=CB（④）。

また、△BCEにおいて、 $\angle CBE=50^{\circ}$ なので、△BCEは二等辺三角形。したがって、BC=CE（⑤）。

ここで、DF=DG-FG、EF=BF-BE。この2つの式と③〜⑤より、DF=EF。よって、△DEFは二等辺三角形。したがって、 $\angle FDE =\angle FED=50^{\circ}$ 。

$x=\angle BDF - \angle FDE=80^{\circ}-50^{\circ}=30^{\circ}$ 。

おわり。

二等辺三角形を作って合同を証明するっていう流れは、中学内容でも出てきますがこれが元ネタだったり？正三角形が出てくるのも面白いですね。

これ以外にもいくつか解き方があるっぽいので、ヒマだったら追記します。

オンライン指導、生徒受付中！2月3月に指導開始の場合、割引！

神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。

体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。