スタンダード数学演習12AB(2018)、「ベクトルと内積」のA問題316の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。
回答例の「方針」や( )内の説明は実際の回答ではないですが、解説のために入れてあります。
(1)の回答例
方針:とりあえず![]() の式に
の式に![]() と
と![]() の成分を代入していくところからスタートしてみる。あとは
の成分を代入していくところからスタートしてみる。あとは![]() と
と![]() のなす角が45°であることから内積を使うことを考える。
のなす角が45°であることから内積を使うことを考える。
(1) 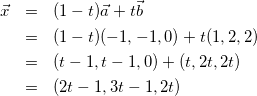
(ベクトルで45°を利用できるものとしては内積くらいしかないので、とりあえず内積の式を作ってみる。)
(2) 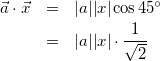
ここで、![]() を成分で計算すると
を成分で計算すると
(3) 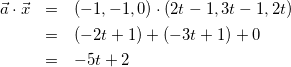
(ここで、式(2)の|![]() |と|
|と|![]() |を計算して
|を計算して![]() をtの式で表せば、式(3)と連立できることがわかる)
をtの式で表せば、式(3)と連立できることがわかる)
(4) ![]()
(5) 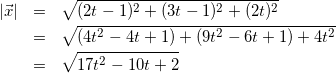
式(4)と式(5)を式(2)に代入して
(6) 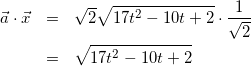
式(3)と式(6)より
(7) 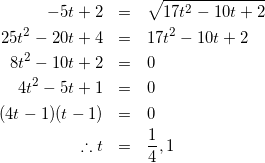
(ここで終わりにしがちだが、求めたtの値が解として適しているか検討しなければいけない)
ここで、t=1のとき
![]()
となる。このとき
![Rendered by QuickLaTeX.com \begin{eqnarray*} \vec{a}\cdot\vec{x}&=&\vec{a}\cdot\vec{b}\\ &=&-1-2\\ &=&-3\\ \\[5pt] \cos{\theta}&=&\frac{\vec{a}\cdot\vec{x}}{|\vec{a}||\vec{x}|}\\ &=&\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\\ &=&\frac{-3}{\sqrt{2}\cdot3}\\ &=&-\frac{1}{\sqrt{2}}\\ \\[5pt] \therefore \theta&=&135^\circ\\ \end{eqnarray*}](https://tutor-blog.com/wp-content/ql-cache/quicklatex.com-17cae268794b1e1c67ef8ce86aa41878_l3.png)
となるので、t=1は解としては不適。
![]() のとき
のとき
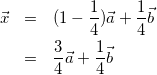
![Rendered by QuickLaTeX.com \begin{eqnarray*} \vec{a}\cdot\vec{x}&=&\vec{a}\cdot(\frac{3}{4}\vec{a}+\frac{1}{4}\vec{b})\\ &=&\frac{3}{4}|\vec{a}|^2+\frac{1}{4}\vec{a}\cdot\vec{b}\\ &=&\frac{3}{4}\cdot2-\frac{3}{4}\\ &=&\frac{3}{4}\\ \\[5pt] |\vec{x}|&=&\sqrt{17\left(\frac{3}{4}\right)^2-10\cdot\frac{3}{4}+2}\\ &=&\sqrt{\frac{9}{16}}\\ &=&\frac{3}{4}\\ \\[5pt] \cos{\theta}&=&\frac{\vec{a}\cdot\vec{x}}{|\vec{a}||\vec{x}|}\\ &=&\frac{\frac{3}{4}}{\sqrt{2}\cdot\frac{3}{4}}\\ &=&\frac{1}{\sqrt{2}}\\ \\[5pt] \therefore \theta&=&45^\circ\\ \end{eqnarray*}](https://tutor-blog.com/wp-content/ql-cache/quicklatex.com-0f8c8f1ea8b0cda367883635d75302d2_l3.png)
したがって、解は![]()
(2)の回答例
方針:![]() を扱いやすいベクトルで表していくのが正解ルートだが、そのためには図を書くことが重要。
を扱いやすいベクトルで表していくのが正解ルートだが、そのためには図を書くことが重要。
(まずは図を書こう。)
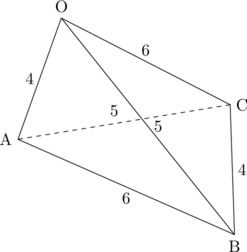
(図はかけたが、その後の方針を定めるために![]() を計算してみる)
を計算してみる)
(8) ![]()
ここで
(9) ![]()
(10) ![]()
(なので、![]() と
と![]() の値が必要になるが、どの面も3辺の長さがわかっているので余弦定理でいけそう)
の値が必要になるが、どの面も3辺の長さがわかっているので余弦定理でいけそう)
△ABCについて
(11) 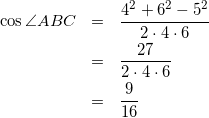
(分母はあえて計算しないのがこういう計算をするときのコツ)
△OBCについて
(12) 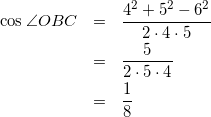
式(11)と式(12)をそれぞれ式(9)と式(10)に代入して
(13) 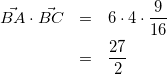
(14) 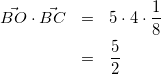
式(13)と式(14)を式(8)に代入して
(15) 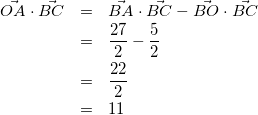
したがって
(16) 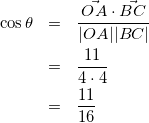
(1)のポイント
(1)最大のポイントは「![]() を2通りの式で表せることに気付けるか」というところですね。
を2通りの式で表せることに気付けるか」というところですね。
これに気づけば「tの方程式が作れる!」→「解けばtが求まる!」と順に進んでいけるはずです。
もう1つのポイントは解の検討をしないといけないところですね。この問題に関しては言われないと気づかない人が多いのではないかと思います。
こういう問題を通して常に解の検討を意識しておくことを学べますね。
(2)のポイント
(2)最大のポイントはこの四面体を書けるかどうかです。図が書けないと△ABC以外の面のcosの値を計算することができません。
あとは、回答例に書いてありますが、まずは内積を計算してみて見通しを立てることが重要です。
おそらくテキストの解答では上述の回答例のような書き方はしてないと思いますが、私は回答例のような進め方が自然だと思いますし、こういう解説を読んで勉強した方がより理解しやすく、身につきやすいと思います。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

