スタンダード数学演習12AB(2018)、「ベクトルと平面図形(1)」のA問題326の解説です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。
回答例の「方針」や( )内の説明は実際の回答ではないですが、解説のために入れてあります。
(1)の回答例
方針:セオリー通り、![]() を既存のベクトルで表していく。
を既存のベクトルで表していく。
(とりあえず図を書きます。それぞれの頂点の位置関係はまだ決まってないので適当で。)
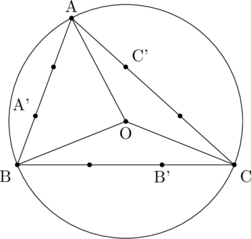
(1) 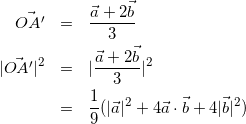
ここで、図形から考えて、![]() なので
なので
(2) 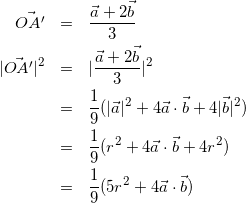
(2)の回答例
方針:正三角形であるための条件から逆算して何をやればいいか考える
(正三角形であるための条件を考えると3辺が等しいか、3つの角が等しいのどちらかっぽい。ベクトルに関係ありそうなのは角度の方。最終的には内積の式に持っていきたい。(1)の流れを考えて手を動かしていく。)
(1)と同様に考えると
(3) ![]()
(4) ![]()
また、A’、B’、C’を通る円の中心をOとしているのでOA’、OB’、OC’はそれぞれ半径になるので
(5) 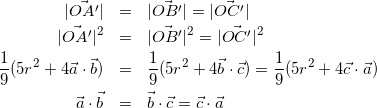
(6) 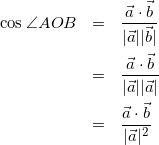
(7) 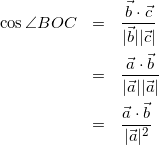
(8) 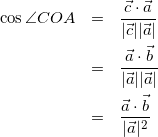
OA=OB=OCであり、式(6)、式(7)、式(8)より![]() なので△ABCは正三角形。
なので△ABCは正三角形。
(1)のポイント
まずは方針に書いてあるようにセオリー通り手を動かすことが大切。途中で![]() であることに気付けるかもポイント。
であることに気付けるかもポイント。
そのためにはざっくりと図を書くことが重要ですね。ベクトルは視覚的に得られる情報も多いので。
(2)のポイント
糸口が見つけづらいので、まずは回答の方向性を考えるところからですね。
「正三角形と言うにはどういう条件が必要か」という点と「ベクトルの問題」であることから考えて内積の式の利用という方向は発想しやすいと思います。
「3点A’、B’、C’を通る円の中心がOと一致する」→「|OA’|=|OB’|=|OC’|」というのも反応すべきポイントですね。
ちなみに図はこんな感じになってるはずです。
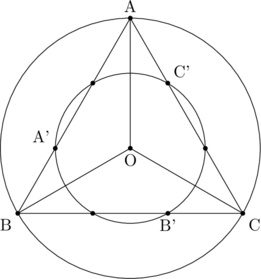
先にこの図を書いてしまうと、うっかり正三角形の性質を証明の中で使っちゃったりするので注意しましょう。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

