スタンダード数学演習12AB(2018)、「ベクトルと内積」の基本問題106の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。
回答例の「方針」や( )内の説明は実際の回答ではないですが、解説のために入れてあります。
回答例
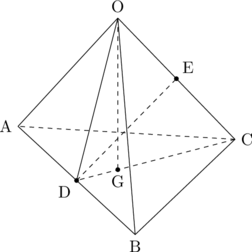
方針:図を書いて考えていく。あとはセオリーどおり。
(まず図を書きましょう)
(1) 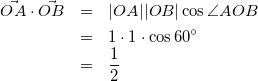
(2) 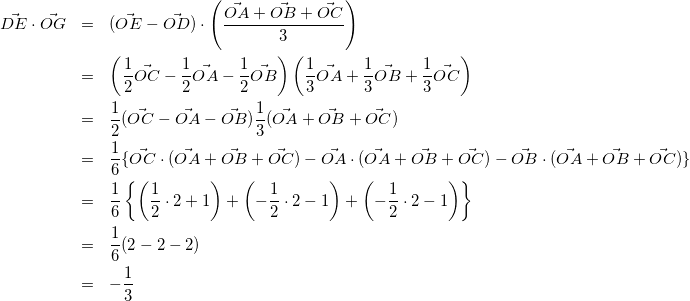
ポイント
![]() は特に難しいところはないですね。内積の公式に当てはめるだけで解けちゃいます。
は特に難しいところはないですね。内積の公式に当てはめるだけで解けちゃいます。
![]() の方は「
の方は「![]() を他のベクトルで表す」ことと「重心のベクトル」の2つに反応できるかがポイント。
を他のベクトルで表す」ことと「重心のベクトル」の2つに反応できるかがポイント。
重心を表すベクトルは反応しやすいが「![]() を他のベクトルで表す」というのは反応しにくい気がします。
を他のベクトルで表す」というのは反応しにくい気がします。
「扱いにくいベクトルは他の扱いやすいベクトルで表す」というのはセオリーなのですぐに手を動かせるレベルにしておこう。今の場合、![]() 、
、![]() 、
、![]() 、の3つは大きさがわかっているしそれぞれの間の角度もわかっているので扱いやすい。
、の3つは大きさがわかっているしそれぞれの間の角度もわかっているので扱いやすい。
また、式(2)の4行目から5行目の計算は、![]() であることと、
であることと、![]() であることを利用しているため回答例のようにカンタンに計算できる。慣れてくれば3行目と4行目もカットできるはず。
であることを利用しているため回答例のようにカンタンに計算できる。慣れてくれば3行目と4行目もカットできるはず。
スポンサーリンク
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

