スタンダード数学演習12AB(2018)、「ベクトルの基本」の基本問題310の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。
回答例の「方針」や( )内の説明は実際の回答ではないですが、解説のために入れてあります。
この問題に関しては回答例よりもポイントを先に読んだ方が理解しやすいと思います。
回答例
方針:交点の位置ベクトルを2通りで表して係数比較すればイケるかも?と考えて手を動かす。
(まずは図を書きましょう)
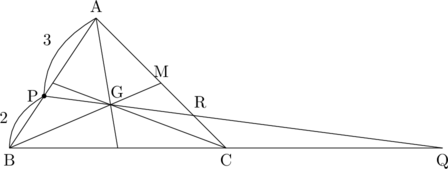
(「最終的には![]() を
を![]() と
と![]() で表したい!」と言われてピンとくるでしょうか?理由はポイントのところで解説します。)
で表したい!」と言われてピンとくるでしょうか?理由はポイントのところで解説します。)
(![]() を
を![]() と
と![]() で表すために、まずは
で表すために、まずは![]() を2通りの式で表していきます。)
を2通りの式で表していきます。)
kを実数として、線分PQと線分ACの交点をRとすると、
(1) 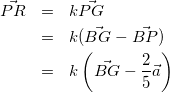
Gは重心なので、BG:GS=2:1。よって、ACの中点をMとして、
(2) 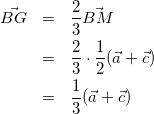
式(1)(2)より、
(3) 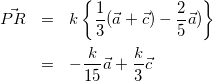
(次は![]() を他の式で表していきます。)
を他の式で表していきます。)
l(エル)を実数として、
(4) 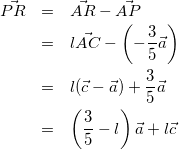
式(3)(4)の係数を比較して、
(5) 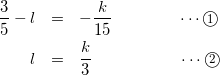
式(5)-②を式(5)-①に代入して、
(6) 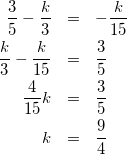
これを式(3)に代入して、
(7) 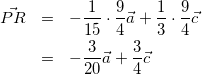
よって、
(8) 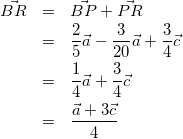
つまり、Rは線分ACを3:1に内分する点なので、AR:CR=3:1
チェバ・メネラウスの定理より、
(9) 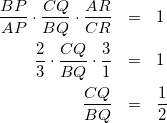
BQ:CQ=2:1なのでBQ:BC=2:1
よって、![]()
ポイント
この問題は正解にたどり着くまでの工程が多いので、最初の段階では「これで解けるぞ!」という方法を思いつくことが難しいです。
そういう問題の場合は、セオリー通りに考え、式を作りながら正解ルートを探していくのが基本です。
思考順序
問題集や参考書の解説は自然な思考順序で書かれていないことが多いので、その解説の真似をしているだけだと学力はあまり上がりません。
下手をすると「暗記」しているだけになり、応用が効かない勉強をずっと続けることになります。
学力を上げるには、例えば、以下のように考えられるようにしておくと良いと思います。
- (図形を見て)チェバ・メネラウスを使いそうだな
- チェバ・メネラウスはここに使えばよさげ(式(9))
- 式(9)から逆算してAR:CRがわかれば良さそう
- AR:CRを知るには
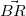 が必要
が必要 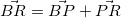
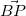 =
=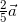 だからあとは
だからあとは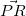 を
を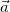 と
と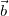 で表せれば良さそうだ
で表せれば良さそうだ
ここまでくれば、![]() を2通りの式で表して係数比較すればいけそうだと思いつくことができると思います。
を2通りの式で表して係数比較すればいけそうだと思いつくことができると思います。
実際にはここまで綺麗に思いつくことは難しいと思いますので、現実的なアプローチの方法としては、まずは式(9)、式(1)、式(4)あたりを作ってみるのが基本動作です。
「式を作ってみたら、次の一手となるアイデアを思いついた」ということはよくありますからね。
少しレベルが足りていない人の特徴
式(9)、式(1)、式(4)あたりを作ってみることを思いつかない人はまだまだ演習不足です。ベクトルの問題でこの図形を書いたら、これらの式を作ってみようと自然と思いつくようになっていないといけません。
とはいえ「チェバ・メネラウス」や「交点を表すベクトル」などそれぞれ単体知識で解くような基本問題ばかりをやっていてもレベルは上がらないので、このレベルの問題演習を繰り返して、基本動作を徹底的に身につけていきましょう。
まったくレベルが足りてない人の特徴
上の解説を読んで、「チェバ・メネラウス」や「交点を表すベクトル」について「なんだっけ?」と参考書や教科書を調べている人はまったくレベルが足りていません。
そういう人はそれぞれ単体知識で解くような基本問題でトレーニングして、上の解説を読んで「なるほど」と思えるレベルになりましょう。
別解
式(7)までは同じですが、そのあと違う流れで解くことができます。
(7) 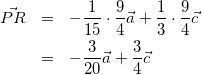
まずは以下のように考えます。
PはABを2:3に内分する点
↓
BPはABを5等分したうちの2個分
↓
つまりBPはABを20等分したうちの8個分
また、式(7)の図形的な意味を考えると、![]() は、線分ABを20等分したうちの3個分だけPからBに進んだ点をSとし、Sから
は、線分ABを20等分したうちの3個分だけPからBに進んだ点をSとし、Sから![]() だけ進んだということになります。このとき、SRとBCは平行になっています。
だけ進んだということになります。このとき、SRとBCは平行になっています。
図で表すとこんな感じになります。
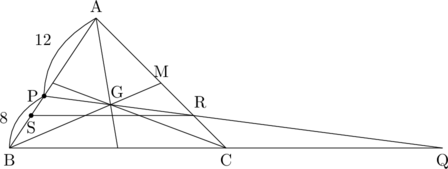
よって、BP:SP=8:3
SRとBQが平行なので△PSR∽△PBQ
よって、BP:SP=BQ:BC=8:3
したがって、
(10) 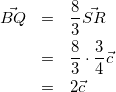
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

