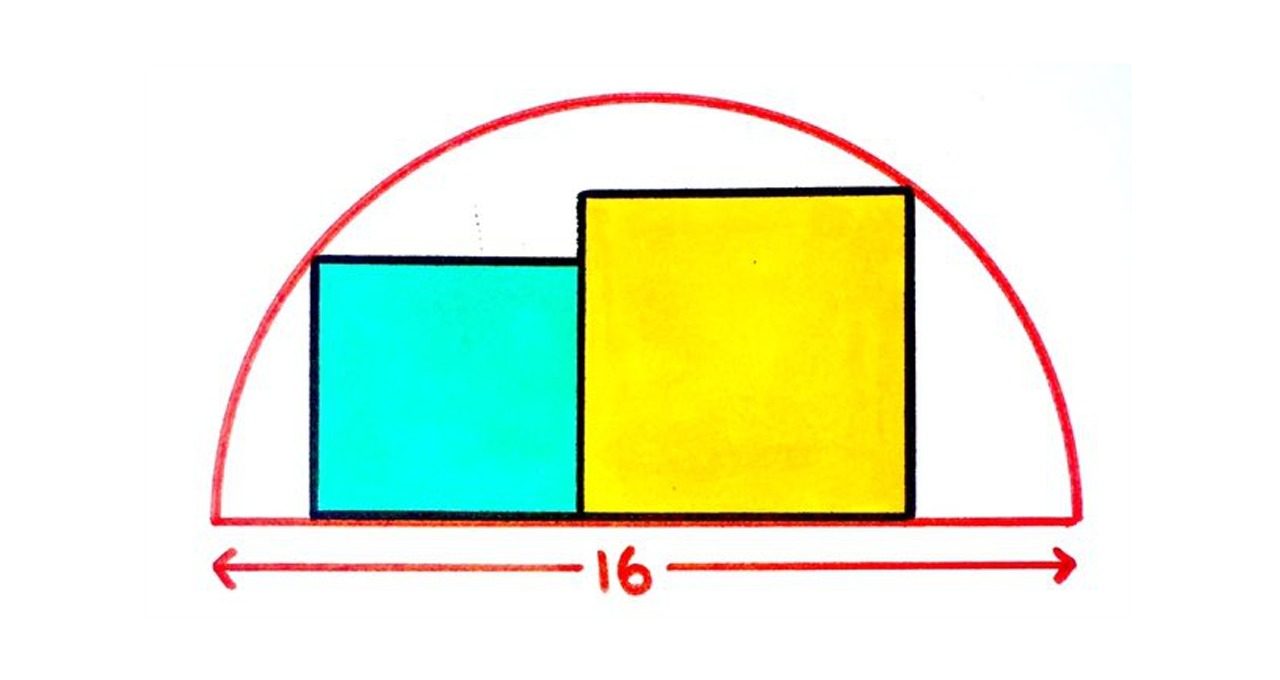
毎度おなじみTwitter問題です。今回は半円に接する2つの正方形の面積に関する問題です。今回もいつもお世話になっているCatrina Shearerさんです。
問題
問題はこんな感じ。
What’s the total area of these two squares? pic.twitter.com/JMbSVKct7u
— Catriona Agg (@Cshearer41) August 24, 2019
一応、問題の画像も載せておきます。
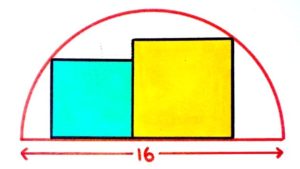
解説
問題の画像のまま解くことも可能ですが、題意からも予想できるように、上記画像のような半円に接する二つの正方形の合計の面積は常に等しいのでそれを利用します。
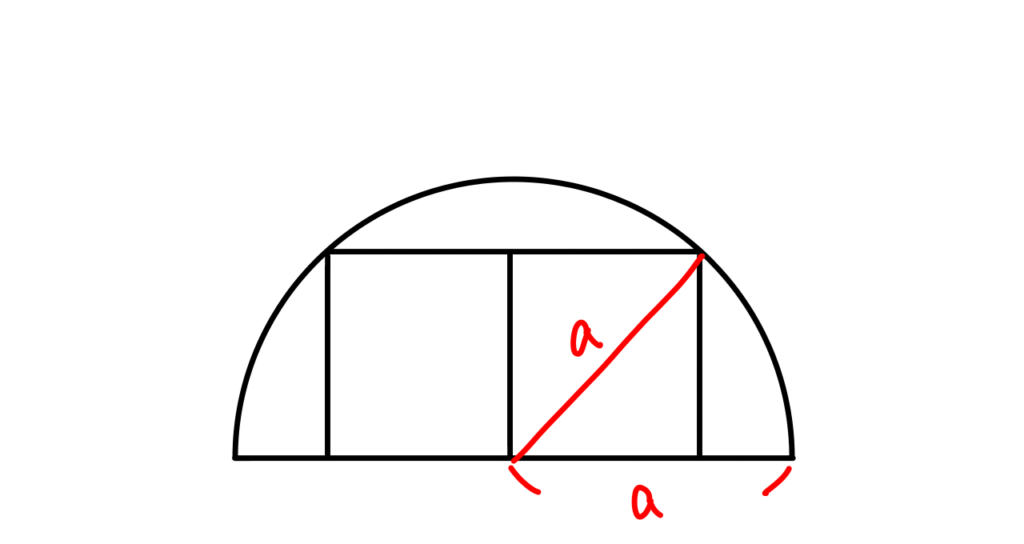
2つの正方形の面積が同じだった場合を考えると上記画像のようになります。ひとつの正方形の対角線で切った場合、その対角線の長さはaです。2つの正方形の合計の面積はこの三角形4つ分なので、
その面積は
となります。元ネタの設定では、直径が16の円なので、面積は8×8=64ですね。
「面積が一定」の証明
上記の解説では「半円に内接する2つの正方形の面積が常に一定」ということを問題文から予想して解いていますが、では本当にそうなのかというのを証明したいと思います。
まず、以下のような三角形（青い線）を考えます。
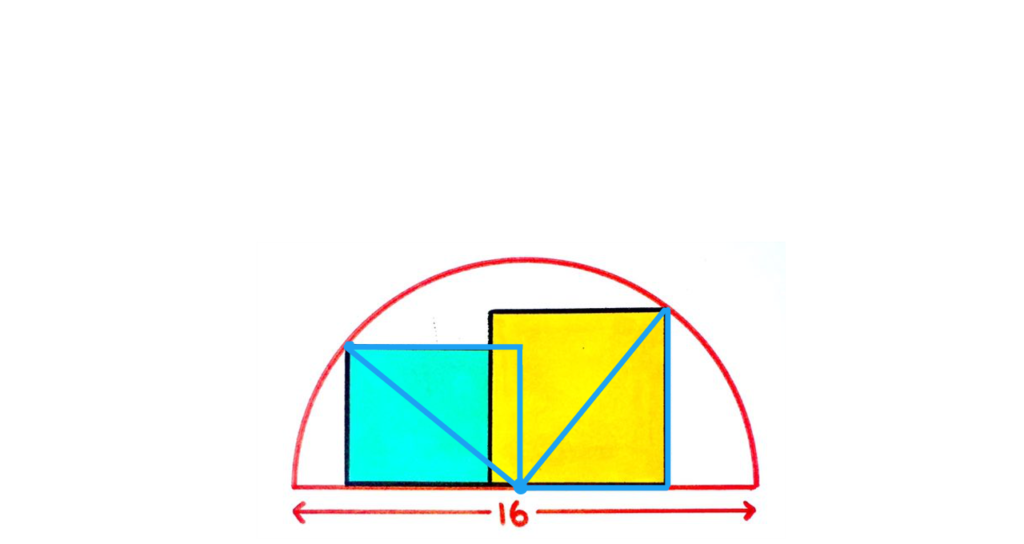
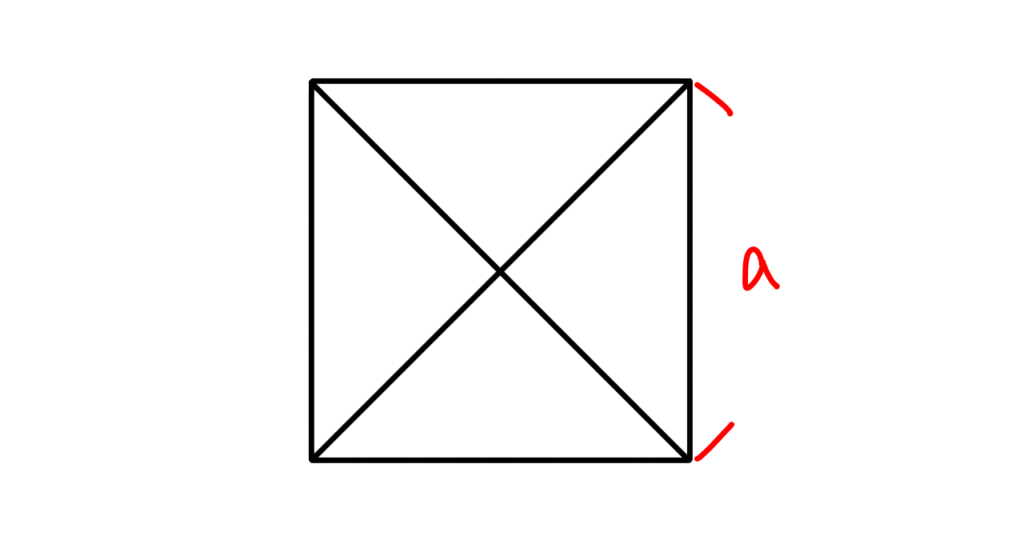
この二つの三角形は90度回転させた図形なので合同です。
次に、この三角形を利用して正方形を作ります。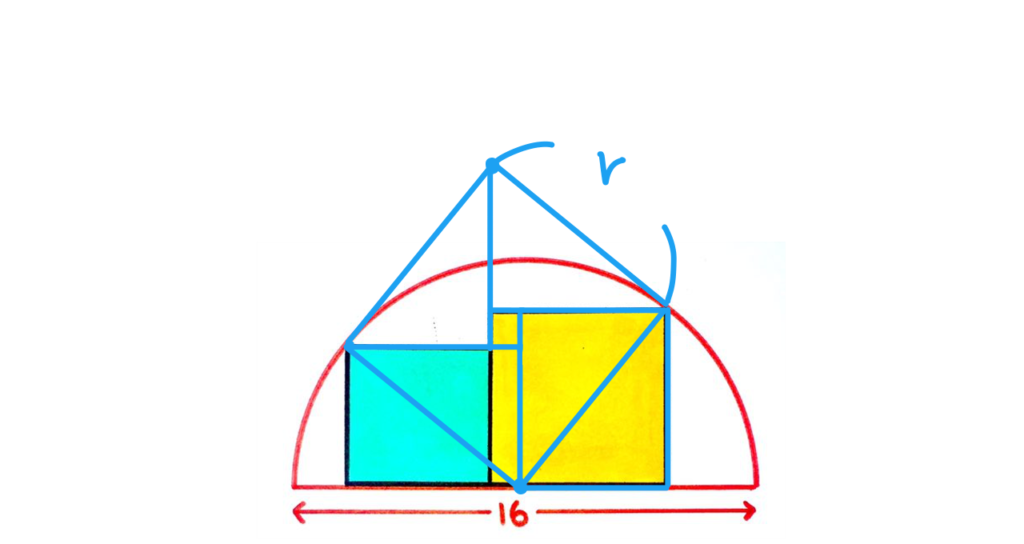
出来上がった正方形の一辺の長さは円の半径（rとする）と等しいので面積は
。これは二つの正方形の面積と一致します。
よって、当該の面積は常に半径の二乗で一定と言えます。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年：中学生、高校生、浪人生
- 指導科目（高校）：数学、物理、大学受験指導
- 指導科目（中学）：数学、理科、高校受験指導
- 指導形態：SkypeまたはZoomによるオンライン指導
- 指導曜日・時間：要相談
- 料金：1時間6,000円（税別）→5,000円（2月3月指導開始の方だけ！）
- 体験指導：60分（ヒアリング含む）
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。
