twitterで数学的素養とは何かを問うようなツイートが流れてきたんですが、なかなか面白い疑問だったので考えてみました。
元ネタ
元ネタはこれ。
こういう問題って、特に情報系の知識がなくとも初見で解けてしまう人と、きちんと説明されないと解けない人に分かれるんじゃないかと思うんですよね。
仮に分かれるとしたら、それは何の差なんだろうか。論理力? 高校数学か物理? センス? pic.twitter.com/4Qhuk5MAR8— Shin Tanimoto / CERO-METAL (@cero_t) August 14, 2019
問題自体は高校レベルの確率の知識などがあれば解けますがそれは主旨ではないので省略するとして、その知識がない人、例えば小学生、がこの問題の答えに辿りつけるとしたらどう考えるのか、を考えてみました。
一応、問題画像を貼っておきます。
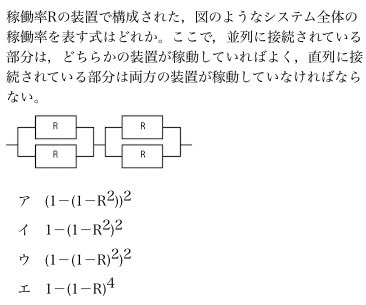
コナンくん的な推理で解く
もし、私が黒ずくめの男に謎の薬を飲まされ、確率や情報系、物理学(回路)の知識がない小学生に戻ってしまったら、次のように考えると思います。
まず、適当な値を代入して計算した表を作ります。

次に以下のように考えます。
1個の場合と2個並列の場合を比較
もしR=0.5なら1個の場合は稼働率は0.5だけど、2個並列の場合はどちらかが稼働してれば良いので稼働率は0.5より大きくなるはず(実際に計算すれば1つの並列部分の稼働率は0.75とわかる)。
1個の場合と2個直列の場合を比較
もしR=0.5なら1個の場合は稼働率は0.5だけど、2個直列の場合は両方とも稼働してなければいけないので稼働率は0.5より小さくなるはず(実際に計算すれば2個並列の稼働率は0.25とわかる)。
「2個直列」と「2個並列を2個直列(問題設定)」を比較
上記2つのことから並列にすると稼働率は上がり、直列にすると稼働率は下がることがわかるのでこの2つの稼働率は「2個直列」<「2個並列を2個直列(問題設定)」というのがわかる。よって、0.5<「2個並列を2個直列(問題設定)」。
r=0.5のときの値が極端な(エ)は除いても良さげ。したがって(ウ)。
(エ)を選択肢から消去するところは根拠が弱いですが、この条件だとこれが限界。
私は小学生に回路の問題を教えるときにこれと同じような考え方を教えるようにしています。「こう計算すれば解ける」ということだけ教え込んでも賢くならないと思うので。
「具体的な数字で計算してみる」や「概数で考える」というのは重要なスキルな気がします。この辺が数学的素養と言えるかもしれないです。知らんけど。
おまけ
おまけで数学的素養を問う問題を。
上記の問題で、2個並列をもう1つ追加し「2個並列×3の直列」にしたとき、任意の稼働率Rに対するシステム全体の稼働率は「2個並列×2の直列」のときと比べて増加するか減少するか。
これも計算すればわかりますが、コナンくん的な推理をすれば計算しなくてもわかりますね。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。