都立高校入試の数学の勉強方法をまとめました。ここに書いてあることを実行すれば確実に目標点を取ることができるようになります。プロとして10年400人以上を個別指導してきた経験からどの目標点にも対応するように解説したので参考にしてみてください。
内容がめちゃくちゃ多いので、目次を見て興味あるところから読むことをおすすめします。目次はリンクになってるのでクリック(タップ)すればそこまで飛べます。
問題構成と配点
都立高校入試の数学は平成25年度〜平成30年度でほぼ同じ出題パターンなので、対策がしやすいです。平成30年度の問題を例に見てみましょう。
| 第1問 | 計算、小問集合 | 5点×8、6点×1 | 46点 |
| 第2問 | Sさんが作った問題 | 5点×1、7点×1 | 12点 |
| 第3問 | 関数とグラフ | 5点×3 | 15点 |
| 第4問 | 平面図形 | 5点×2、7点×1 | 17点 |
| 第5問 | 空間図形 | 5点×2 | 10点 |
注目すべきは第1問だけで46点分もあることです。計算だけでも30点分あるので計算は最優先で勉強しておきましょう。しかも計算問題も他の問題と同じように1問5点なのでお得です。
第1問、第3問〜第5問は出題単元がずっと同じですが、第2問だけは年度によって異なるので対策に時間がかかります。数学が苦手な人は後回しにした方が良いでしょう。
以下で詳しく解説します。
他の年度の問題はこちらからどうぞ。
第1問:計算
平成30年度の第1問の計算問題はこんな感じです。

第1問の計算は5点×8問、合計30点です。計算さえできれば40点も取れるのはオイシイので、最優先で計算練習しましょう。
計算の出題パターンは以下の通りです。
- 正負の数(加減乗除、分数あり)
- 文字式(カッコあり)
- 平方根(展開or有理化)
- 1次方程式(カッコあり、移項あり)
- 連立方程式(だいたい加減法)
- 2次方程式(因数分解or解の公式)
計算問題についてもほぼ毎年同じ形なので対策しやすいです。ある程度計算ができる人なら過去問だけやるだけでも十分点数が取れるようになるはずです。
(1)は毎年同じ形で「正負の数の加減」と「分数と整数の乗除」のスキルが問われます。「乗除の方から先に計算する」など基本的な知識をしっかり身につけましょう。
(2)も毎年同じ形で文字式の計算ですが、カッコを含む計算のスキルが問われます。「ー(AーB)=ーA+B」の式変形をできるようにしておきましょう。
(3)は平方根の計算ですが、展開と有理化が交互に出題されています。平成30年度は展開なので平成31年度は有理化が出題される可能性が高いです。もちろん、どちらでも対応できるようにしておいた方がリスクは低くなります。
(4)は毎年ほぼ同じ形で1次方程式で、カッコあり、移項ありの問題が出題されています。平成30年度になってなぜかカッコがなくなりましたが、平成31年度では復活する可能性もあるのでカッコありの計算もできるようにしておいた方が良いでしょう。
(5)は連立方程式です。ほぼ加減法の形で出題されています。加減法か代入法、どちらで解くかの指定は特にないので自分が解きやすい方で解く練習をしておきましょう。
(6)は2次方程式です。左辺を因数分解して解くパターンと解の公式で解くパターンが交互に出題されています。平成30年度は因数分解パターンだったので平成31年度は解の公式パターンが出題される可能性が高そうです。もちろんこの問題もどちらの方法でもできるようにしておいたほうが良いですが、最悪、解の公式で全て解けるので解の公式だけできるようにしておけばOKです。
計算の勉強方法
第1問の計算の出題パターンがわかったので次は計算の勉強方法について解説します。以下の流れで勉強するのがセオリーですね。
- 計算用の教材や総合問題集で計算だけ練習する
- 過去問の計算部分だけ前年度分解く
計算の出題パターンはほぼ決まっているので、まずは①で基本スキルを身につけましょう。そのあとは過去問の第1問の計算問題だけ前年度解いて実力を身につけます。もちろん、1年度分解いたら○付け&間違えたところを他の教材で復習というのは必ずやりましょう。
計算練習でオススメの市販教材を紹介しておきます。
計算は計算だけの教材でトレーニングするのがベストです。この教材は中1、中2、中3と分かれているので必要なものだけ選んで使うことができます。小学生が使うようなドリルですが効果はバツグンです。
計算は目標が何点の人でも100%正答したいので「たくさん練習できる&出題傾向以外も練習できるもの」を使うのがセオリーですが、時間がないときは以下の教材がオススメです。
第1問:小問集合
平成30年度の第1問、問7〜問9の小問集合はこんな感じです。

問7は「資料の整理・データの分析」or「変域」or「変化の割合」の3パターンが出題されています。
問8は「角度を求める問題」or「確率」の2パターンが出題されています。
問9は毎年、作図です。
第1問:小問集合の勉強方法
ここは以下のように勉強を進めると良いでしょう。
- 問7対策として「資料の整理・データの分析」「変域」「変化の割合」を練習する
- 問8対策として「角度を求める問題」「確率」を練習する
- 問9対策として「作図」を練習する
各単元をバラバラに勉強するよりも「まずは問7対策をしよう!」と思って勉強した方が効果的です。
問7〜問9はどれも基本的な問題ばかりなので一般的な問題集で十分対策できますが、問9の作図は少しだけコツをおさえておくと正答率がグッと上がります。
作図も平成25年度〜平成30年度の問題を見てみると何を優先して勉強すれば良いか見えてきます。
- 平成25年度:3点から等しい距離にある点の作図(垂直二等分線)
- 平成26年度:三角形を90°回転させる(垂直)
- 平成27年度:三角形の面積を二等分する直線(垂直二等分線)
- 平成28年度:点Pを頂点とする正方形の作図(垂直)
- 平成29年度:扇型の弧を3:1に分割する点Pの作図(角の二等分線)
- 平成30年度:2点を重ねる時の折り目の作図(垂直二等分線)
カッコ内に書いてあるのは解くために使うスキルです。どうやら都立高校入試の問題は垂直が好きみたいですね(笑)。
気をつけなければいけないのは『問題文や図には「垂直二等分線を用いること」は書いていない』ということです。問題文や図を見て、自分で判断しなければいけないのでやや難易度が高いです。配点が6点の理由はそこですね。
『「3点から等しい距離にある点」ときたら「垂直二等分線」だ!』のように問題文のキーワードに反応して何を使うか判断する練習を日頃から意識的に行うと、本番でも解けるようになります。この練習は小問集合だけではなく、あらゆる場面で使える勉強テクニックなので覚えておきましょう。
小問集合の勉強をするのにオススメの教材を紹介しておきます。
これは公立高校入試の小問集合対策用の教材です。都立高校入試の傾向問題を優先して練習しましょう。
第2問:Sさんが作った問題
平成30年度の第2問はこんな感じです。
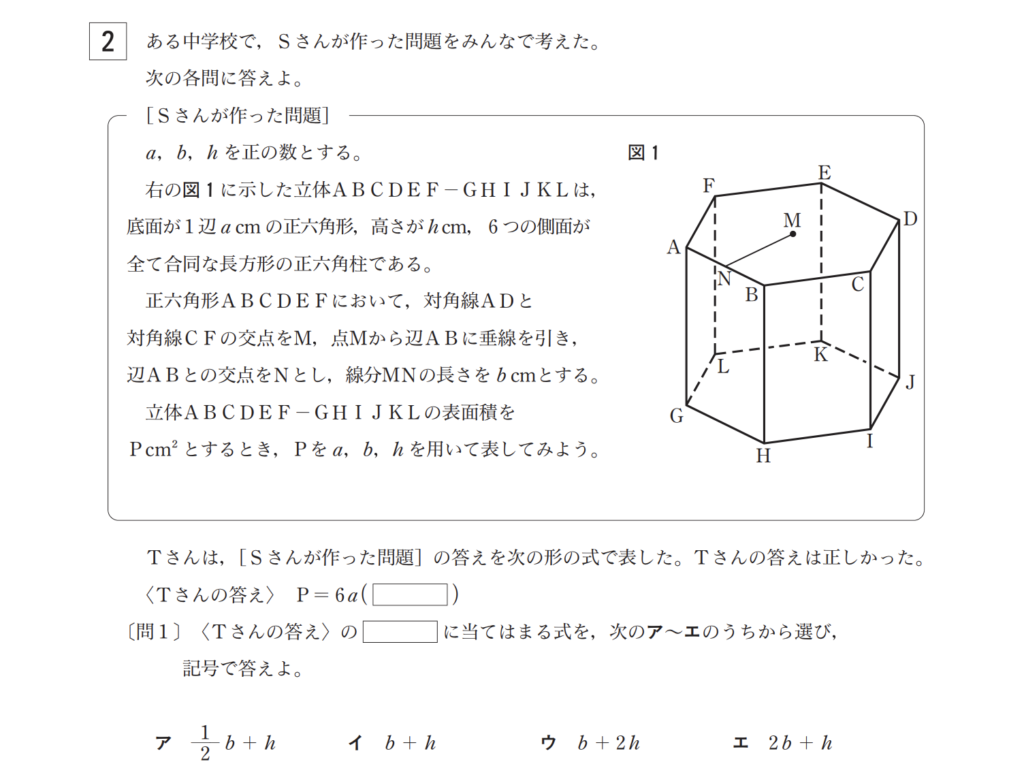
第2問はいわゆる「Sさんが作った問題」です。問1、問2それぞれの出題パターンは以下の通りです。
問1
- 式を立てる問題(H30、H27)
- 場合の数(H28、H26)
- 側面積(H25)
- ひたすら書き出す(H29)
問2
- 等式の証明
問1が厄介です。平成25年度〜平成30年度の6年間で大きく分けて4パターン出題されているので、どのパターンがくるか予想しにくいです。これら以外の問題パターンが出題される可能性もあります。とりあえず、これらの出題パターンは優先して勉強するようにしましょう。
問2は等式の証明でほぼ決まりと考えてOKです。問1をヒントにして解くように設定されていますが、それができるのは学力が高めの人だけですね。
第2問の勉強方法
第2問は主に次の知識が必要なので、持っている教材で該当する単元を探して練習しておきましょう。特に、面積を文字式で表す練習は必須です。
- 表面積の求め方(立式)
- 側面積の求め方(立式)
- 台形の面積の求め方(立式)
- すい体(立式)
- 整数nを使った式(立式、証明)
この辺の知識を理解するには教科書使うのが一番良いですが、1年とか2年の教科書捨てちゃって持ってない人は以下の3つがオススメです。
この3つはだいたい同じなので好きなやつを選んでOKです。中学3年間の内容が全て入っているので、わからないことを調べる用に一冊持っておくと便利です。それぞれ問題集もあるので演習したい場合は合わせて使うと効果的です。
第3問:関数とグラフ
平成30年度の第3問はこんな感じです。
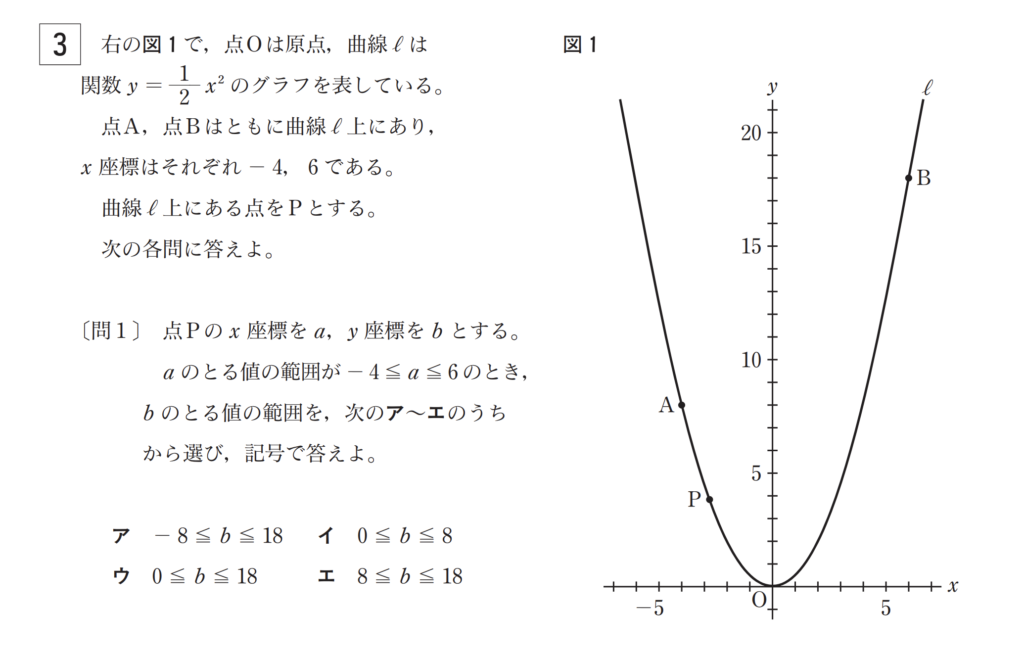
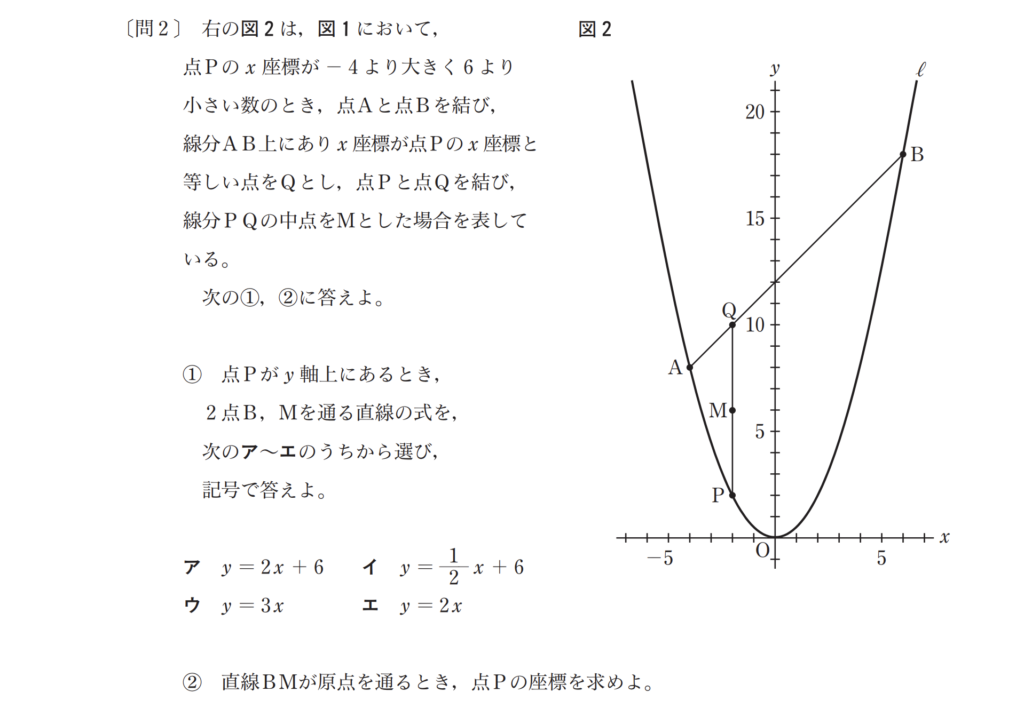
第3問は関数とグラフでほぼ決まりです。年度によって問2までの場合と問3まである場合があります。出題パターンは以下の通りです。
- 変域(H25、H26、H28)
- 座標(H27、H29)
- 直線の式(H25、H26、H27、H28、H30)
- 面積を条件とした直線の式や座標など(H25、H26、H27、H28、H29)
- 原点を通る直線と座標(H30)
変域、座標、直線の式、面積を条件とした直線の式や座標は優先して練習しておきましょう。これらのうち1〜2問は必ず出題されます。平成30年度だけ最後の問題の出題傾向が変わりましたが、原点を通る直線は教科書にも載っている基本事項なのでおさえておきましょう。
関数とグラフを強化したい場合は以下の教材がオススメです。
これらのシリーズは場合の数、確率、図形などもあるので単元ごとの対策をするのに便利です。上のやつの方が量が多いので、必要に応じて使い分けましょう。
第4問:平面図形
平成30年度の第4問はこんな感じです。

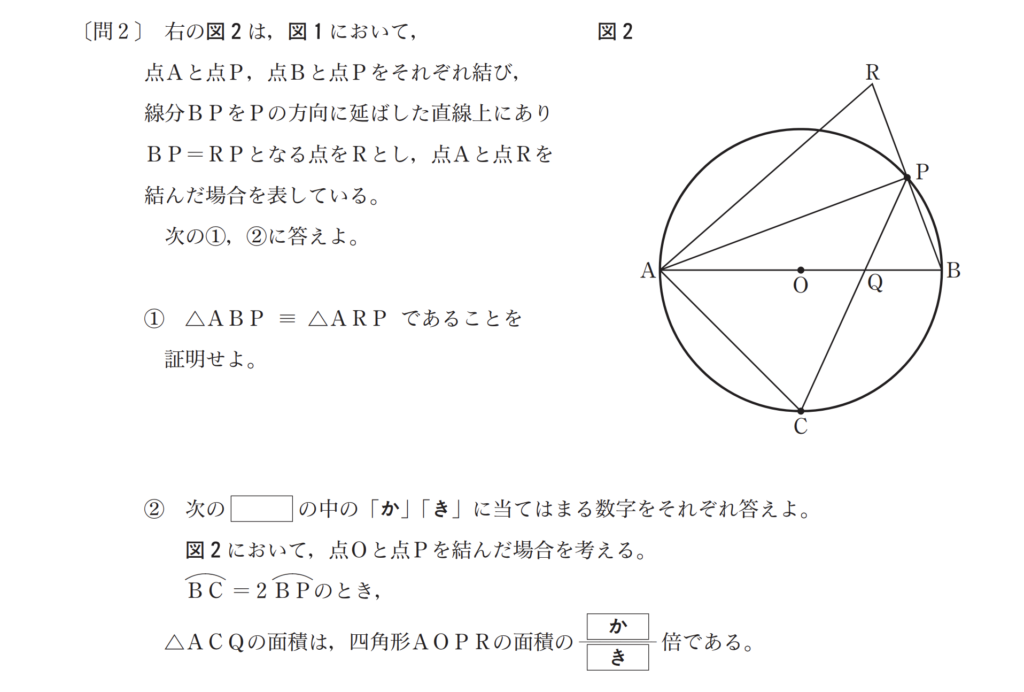
第4問も少し厄介です。主に中2〜中3の平面図形から出題されていて、ピンポイントでの対策が難しいので、幅広く勉強しないといけません。とはいえある程度の傾向はあるので、それをおさえた勉強をすれば効果的です。
問1は平面図形の角度に関する問題が多いです(平成29年度だけ弧の長さを求める問題)。さらに、平成25年度〜平成30年度の問題全てが具体的な数値で角度を求めさせるのではなく、「文字aを用いて表せ」という問題です。
問2は「相似証明→面積比」or「相似証明→長さ求める」のどちらかです。難易度としては標準的な問題なので、練習すればある程度は解けるようになるはずです。
教材は上記のシリーズのやつがオススメです。
(2019/07/15 22:39:13時点 Amazon調べ-詳細)
第5問:空間図形
平成30年度の第5問はこんな感じでした。
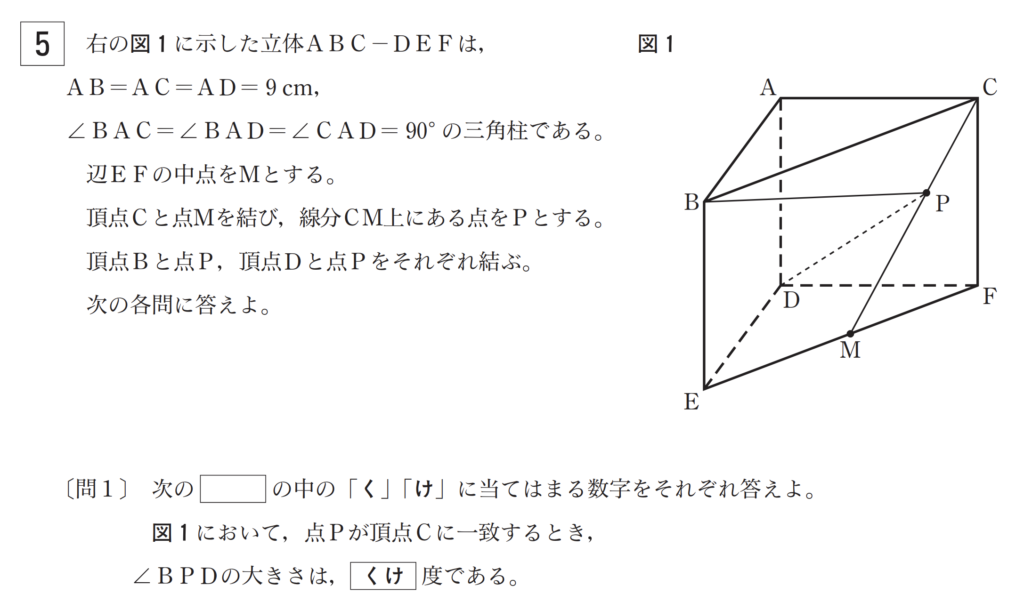
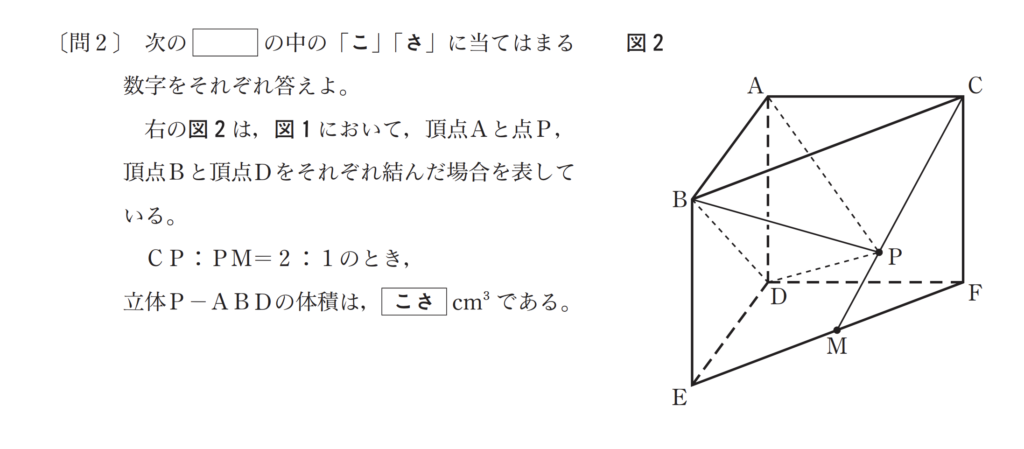
第5問は空間図形ですね。ここは第4問に比べると問題パターンが限られているので対策しやすいです。
問1の問題パターンは以下の3つです。
- 角度を求める(H26、H27、H30)
- 長さを求める(H29中点、H28最短距離)
- 面積比(H25・第4問で出題されてない場合?)
角度を求める問題の場合、複雑な計算は必要ないです。問題の条件から判断して該当する三角形が正三角形か直角三角形であることがわかれば答えられる問題です。わからなかったら三角形の代表的な角である、30°、45°、60°、90°、のうちそれっぽい角度を答えておくようにしましょう。確率25%で当たります(笑)。
長さを求める問題は中点か最短距離の問題が出題されているので、優先的に練習しておきましょう。
平成25年度のように面積比を問われる場合もありますが、これは第4問で面積比の問題がない場合のみだと思います。ということは面積比は第4問か第5問で高確率で出題されるということなので、優先的に勉強しておかないといけませんね。
問2の出題パターンは「体積」でほぼ決まりです。特に「すい体の体積」が出題されると考えてほぼ間違いないでしょう。元の図形は三角すいの場合と直方体の場合がありますが最終的に求める体積は「三角すい」か「四角すい」のどちらかですね。ここは「三平方の定理」のスキルを使う場合もあるのでしっかり練習しておきましょう。
教材は第4問のところで紹介したものを使いましょう。
総合問題集
ここまでに紹介した教材は単元ごとや出題パターンごとの対策用でしたが、ここでは一冊で入試対策を一通りできる教材を紹介しておきます。
どちらか一方を選べば良いですが、個人的におすすめなのは「超効率問題集」の方です。
計算用の教材や単元ごとの教材は総合問題集と過去問をやってそれでも不足する場合に購入するのがセオリーです。最初から単元ごとの教材に手を出すと、時間が足りなくなる可能性があります。また、受験勉強の軸は過去問にあるので、まずは全体像を把握し、その中で自分に必要なところを強化していくのが賢い勉強方法ですね。
模試
模試は定期的に受けた方が良いです。「W合格もぎ」と「Vもぎ」が有名ですね。塾に通っている受験生はこのどちらかを受けている人が多いと思います。
実はこの二つの模試はネットで購入することができます(以下のリンク先参照)。
塾に通ってなかったり、ギリギリで通い始めた人は自分で模試を購入して練習するとかなり効果的です。過去問と合わせてやれば入試対策はバッチリです。もちろん、判定や偏差値は算出されないのでその点は実際に模試を受けるのには劣りますが、本番に限りなく近い形での問題演習は効果的です。
模試の活用方法
模試は「実力チェック」「合格判定を見るもの」ですが、「最大の復習チャンス」と考えておくとより効果があります。以下のことを実行すれば必ずレベルが上がります。
- 模試を受けたその日に自己採点する
- すぐに解説を読んでできる限りの問題を理解する
- 解説を読んだらすぐに解き直す
- 1週間後に解き直す
模試は受験生にとって本番同様のトレーニングをするための唯一のチャンスです。模試を受けた直後にちゃんと復習することで、いつもの勉強以上に身につきます。解説を読むだけではなく、必ず解き直すようにしましょう。解説を読んで「理解したつもり」になる生徒は驚くほど多いですから。①〜③をやっている人はいると思いますが、④をやっている人は少ないです。時間がたったあとで解けるかどうかを確認するのは勉強では非常に重要です。
①〜③はできれば模試を受けた当日にやりましょう。疲れてできない場合でも翌日には必ずやるようにしましょう。受けた直後のほうが「解けた問題」「解けなかった問題」「よくわからなかったところ」などが頭に残っていますからね。
塾教材について
最初の方で書きましたが、市販の教材よりも塾の教材の方が圧倒的に優秀です。なぜかというと市販の教材は全国の公立入試全般に対応した教材しかありませんが、塾教材は神奈川県の入試に特化しているからです。下記の教材はその代表例です。この教材を使うためだけに塾に通う価値はあります。
オリジナルの教材を使っている塾も少なくないですが、それもかなり有効です。私の経験上、講師の質は当たり外れ(とくに外れ)が大きいのでその点では塾に通うメリットはあまりありませんが、塾の教材はその価値が大いにあると言えます。
ちなみに私は仕事柄、これらの塾教材を入手することが可能なので、私の生徒には市販教材ではなく必ず塾教材を使わせています。ホントにかなりの差がありますからね。特に学力的に中の上以下の生徒は結果に大きな差が出ます。
基本的な勉強方法
基本的な勉強方法を解説しておきます。ここに書いてある方法を実行すれば確実にレベルが上がるので参考にしてください。
- 「3回復習」する
- 1週間単位で勉強する
- ○△×で管理する
- 最初に過去問研究する
- 出題傾向ごとに勉強する(過去問をヨコに使う)
- 最後に本番同様のトレーニングをする(過去問をタテに使う)
以下で一つずつ紹介していきます。
「3回復習」「1週間単位の勉強」「○△×で管理」について
受験勉強に限らず、勉強で最も重要なのは復習です。以下のように勉強することで、しっかり定着するようになります。
- 月曜日:勉強する→自分でテストする→寝る前にテストする
- 火曜日:月曜日の内容をテストする→勉強する→自分でテストする→寝る前にテストする
- 水曜日:火曜日の内容をテストする→勉強する→自分でテストする→寝る前にテストする
- ・・・
- 日曜日:月曜〜土曜の内容をテストする
「復習する」だと見て終わりにしてしまう人も多いですが、それでは身につきません。効果のある復習は自分でテストすることです。
毎回全ての問題をテストするのは時間的に厳しいので、テストすべき問題を自分で判断しないといけません。そのために解いた問題は○△×の印をつけて管理しましょう。「○:100%OK」「△:微妙」「×:解答見てもさっぱりわからん」みたいな分け方にするのが基本ですね。
この勉強方法はどの科目でも使える基本中の基本なので、身についていない人は受験勉強を機に身につけておきましょう。そうすれば高校へ入っても勉強で困らなくなりますよ。
最初に過去問研究する
入試の問題はある程度の傾向があるので、まずは過去問を見てどの辺を勉強すれば良いのかを研究するのが最優先です。出題傾向を知った上で勉強することで「あ、これは過去問に載っていたパターンだな」と意識して勉強できるのでより頭に残りやすくなります。
出題傾向についてはすでに詳しく解説しましたが、必ず自分でも確認するようにしましょう。
過去問を購入するときは「掲載年数が多いもの」を選ぶようにしましょう。過去問演習で最も重要なのはたくさん解くことですからね。市販のものでは以下の教材がオススメです。
(2024/04/24 14:36:13時点 Amazon調べ-詳細)
ま、一番有名なやつですね。7年分あるので十分トレーニングができます。
出題傾向ごとに対策する(過去問をヨコに使う)
受験勉強は出題傾向ごとに対策して得点を積み上げていくのが基本です。ここで重要になるのが過去問の使い方です。そのやり方は、実は「計算の勉強方法」のところで解説してありますが、もう一度、第3問・関数とグラフを例にして解説します。
- 単元ごとの教材や総合問題集で関数とグラフの部分を練習する
- 過去問の第3問・関数とグラフを全年度分解く
基本はこれだけです。まずは①で基本スキルを身につけて、そのあと過去問の第3問だけを一気に解きます。もちろん1年度分解いたら○付け&わからないところは他の教材で復習というのは必ずやりましょう。
年度をまたいで出題傾向ごと、大問ごとにトレーニングするので私はこの勉強方法を「過去問をヨコに使う」と表現しています。
これをやるだけでかなりレベルが上がります。もったいないから過去問は最後までやらずにとっておきたくなりますが、過去問を基準に勉強するのが最も効果的です。
これを各大問ごとにやるだけです。
最後に本番同様のトレーニングをする(過去問をタテに使う)
すでにお分かりかと思いますが、最後は年度ごとに過去問を通しで解いていきます。最後の仕上げですね。このときは必ず時間を測って演習しましょう。
ここまでの勉強がちゃんと実行できていれば、ここは確認作業みたいなものです。すでに解いたことがある問題なので時間内に目標点分を解けるかどうかチェックしましょう。1年度分解いたら○付け&復習。これを繰り返すだけです。
得点すべきところができていない場合は最優先で復習するように。
目標〜50点の場合の戦略
目標〜50点の人は以下の流れで勉強しましょう。
- 第1問の計算対策
- 第1問の小問集合対策
- 第3問〜第5問の問1対策
- 過去問演習(仕上げ)
計算だけで30点あるのでここでどれだけ得点できるかにかかってます。最低でも1ミス(25点/30点)でおさえたいところ。
第1問の小問集合は3問中2問を目標にしましょう。第1問で35点/40点取れれば、あとは第3問〜第5問の問1だけ解ければ50点/100点になります。
それぞれの勉強方法は上で書いたことを参考にしてください。
目標〜70点の場合の戦略
目標が〜70点の場合は以下の流れで勉強しましょう。
- 第1問の計算対策
- 第1問の小問集合対策
- 第3問〜第5問対策
- 第2問対策
- 過去問演習(最後の仕上げ)
第1問対策までは目標〜50点の場合と同じです。目標が〜70点の場合は第2問以外は一通りトレーニングしておいたほうが良いですね。第3問〜第5問は好きなところから初めて良いです。勉強しながら「自分が解けるようになりそうなところとそうじゃないところ」をしっかり把握していくことが重要です。
第2問は上述の通り対策するのに時間がかかるので最後にやるようにしましょう。最悪捨てても良いです。
目標〜80点の場合の戦略
このレベルになると、1〜2問のミスや解けない問題が出ることを想定して、出題傾向にある問題を一通り全て解けるようにしないといけません。
基本的には目標〜70点の流れと同じでOKです。あとは元々の学力によってどこまで到達できるかに差があるだけですからね。
まとめ
最後にまとめておきます。
- 計算だけで30点もある
- 第1問だけで46点もある
- 第2問は対策しにくいので後回し
- 第3問〜第5問は出題傾向がほぼ決まってる
- 3回復習、1週間単位の勉強が重要
- 過去問はヨコとタテで使い分ける
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。