知る人ぞ知る参考書ではあるけど、具体的にどういう教材なのかわからない「入試数学の掌握」について徹底的に分析してみました。どんな内容なのか、どういう特徴があるのか、受験生の抱えるどんな課題をどう解決してくれるのか、などこれでもかっていうくらい詳しく解説しました。
「入試数学の掌握」の構成と難易度
「入試数学の掌握」は主に「例題」、「問」、「Check」、の3つから構成されています。
各テーマに沿った「例題」とそれに関連した「問」「Check」があります。「問」の中には解答ありのものとなしのものがあります。解答なしのものは解説するまでもない問題的な感じの扱いですね。
この教材は明らかに最難関校を目指す人の中でも特に数学を強化したい人か、それとは逆に最難関校を目指しているけどなかなか数学の得点が上がらない人向けです。その理由は下記内容を読めばわかります。
「入試数学の掌握」の問題数
この教材に関しては問題数で語る意味があまりないですが、気になる方もいると思うので一応載せておきます。
入試数学の掌握 総論編
- 例題:19題
- Check:25題
- 問:12題
- 足腰の鍛錬のために:4題
- 合計:60題
入試数学の掌握 各論練磨編
- 例題:15題
- Check:22題
- 問:14題
- 合計:51題
入試数学の掌握 各論実践編
- 例題:17
- Check:28
- 問:23
- 足腰の鍛錬のためにリターンズ:2
- 合計:70題
例題、問などは以下の画像のようになってます。



解答方針は以下のようにさらに細かい「鉄則」で解説されているものもあります。

「入試数学の掌握」は東大、京大、阪大を志望する受験生向けの教材
最難関校の入試問題の中でも受験生が苦手な「全称命題」と「存在命題」に特化して解説した教材が「入試数学の掌握」です。特に、東大、京大、阪大に特化した教材です。
「入試数学の掌握 総論編」で基本的な考え方を身につけるための教材です。
「入試数学の掌握 各論練磨編」ではさらに東大、京大、阪大に特化しています。
「入試数学の掌握 各論実戦編」はその場の賢さを問われる問題、つまり総論編や各論練磨編で学ぶようなあらかじめ準備すればある程度解けるような問題ではなく、臨機応変に対応しないと解けない問題を扱っています。特に、東大理3、京大医学部、阪大医学部に特化した内容になっています。
「総論編で全称命題と存在命題の基本的なアプローチを学び、練磨編と実戦編でそれを深掘りしていく」と考えてくれればOKです。
ということで、「入試数学の掌握」は東大、京大、阪大、特に東大理3、京大医学部、阪大医学部を目指す人向けの教材です。国公立医学部志望の人も使って良いと思います。
ほとんどの人にとっては縁のない教材ですね(笑)。
「入試数学の掌握 総論編」の概要


「入試数学の掌握 総論編」は、ざっくり言うと、受験生が苦手な問題パターンを分類して、「こうきたら、こうする!」みたいな感じで解説してます。
私も同じような考え方なのでとても共感します。結局のところ、採点する問題である以上、解けるので、解き方もある程度絞られるわけです。その解法を分類して実行できるようにしておけばほとんどの問題に対応できるようになります。あとは、理解力と記憶力の問題。
ということで、「入試数学の掌握 総論編」がどんな方向性の教材なのかを理解してもらうために、本文を引用しておきたいと思います。一部、理解しやすいように改変している部分もあります。
テーマ1:全称命題
「任意の〇〇について△△が成り立つ」という形のものを”全称命題”と呼ぶ。
全称命題をさらに証明問題と求値問題に分け、それぞれの解答方針を以下のように分類する。
全称命題の証明問題
「任意の〇〇について△△となることを示せ」の回答方針は以下の5つに分類される。
① 不等式の証明(連続量)
→ f(x) = 大きい方 – 小さい方の最小値 ですら0以上を示す。
② 2変数命題の証明(連続量)
→ 領域を導入して、集合の包含関係に持ち込む。
③ nに関する離散命題P(n)の証明(離散量)
→ 数学的帰納法の利用。
④ 整数に関する証明(離散量)
→ 剰余系の利用。余りで整数を分類してすべての場合を尽くす。
⑤ 背理法の利用
全称命題の求値問題
「任意の〇〇について△△となるように範囲を求めよ」の回答方針は以下の4つに分類される。
① 変数について整理し、係数比較の考え方。
② 特別な場合について考え、必要条件を絞り十分性の確認。
③ 恒等式は微分しても恒等式(積分方程式や正式の割り算など)。
④ 領域による視覚化。
テーマ2:存在命題の扱い
存在命題とは「〇〇が少なくとも1つ存在することを示せ」や「ある〇〇に対して△△が成り立つことを示せ」のような問題。
存在命題の回答方針は以下の5つに分類される。
- ディリクレの部屋割り論法(離散量)。
- パラメータを導入して方程式を立て、実数解をもつことを言う(連続量)。
- 題意を満たす具体的なものを1つ見つけて明記してしまう、もしくは具体的に作成する方法を提示する。
- 背理法の利用。
- 数学的帰納法(全称との複合問題)。
引用終わり。
こんな感じですね。これを読んだだけでも頭が痛くなる人もいると思いますが、そういう教材なんです(笑)。
「入試数学の掌握 総論編」は「Theme1 全称命題の扱い」と「Theme2 存在命題の扱い」に分かれています。それぞれのテーマで上記の解法の基本的なアプローチを学びます。
「入試数学の掌握 各論練磨編」の概要


「入試数学の掌握 各論練磨編」は上記画像の目次のように3つのテーマに分けられています。
存在命題をさらに以下の画像のように分類し、それぞれを深掘りしていきます。
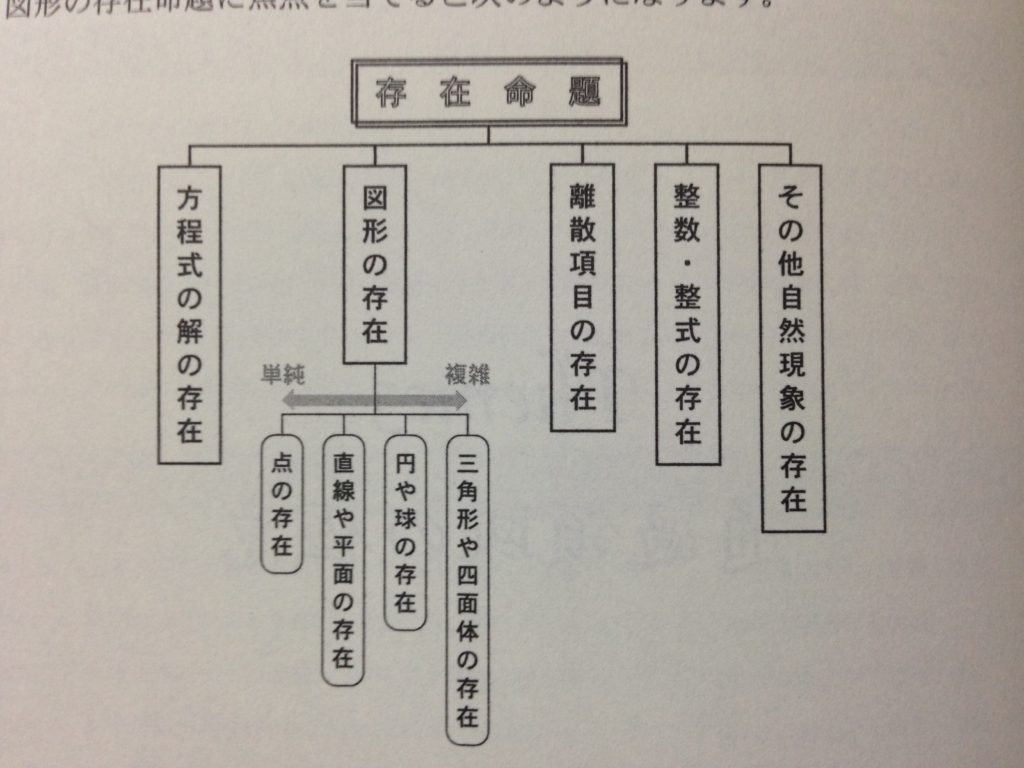
「Theme3 通過領域の極意」は頻出だけど苦手な人が多い
Theme3では上記分類の「点の存在」だけに絞っています。最も単純なものであるにも関わらず、多くの受験生が苦手なことから、テーマ1つ分の紙面を割いているようです。
例題はこんな感じ。

「Theme4 論証武器の選択」は解答方針を引き出す力を養成するパート
Theme4ではこれまでに学んだ全称命題と存在命題の解法のうちどれを使って解くのかを考える力を養成するパートと考えてくれればOKです。
入試本番では、「解法はこうだよ」と教えてくれる人はいないので、問題を解きながらどの解法を使うべきかを考えなければいけません。
当たり前ですが、教材を使って勉強しているときはこの点を忘れがちで、ついついできるようになった気がしてくるので注意が必要です。
Theme4の例題はこんな感じです。

「Theme5 一意性の示し方」は「ただ1つ存在することを示せ」の対処法を学ぶパート
テーマ5は存在命題を補完するために「〇〇がただ1つ存在することを示せ」という問題へのアプローチ方法を学ぶパートです。
この問題パターンもよく見ますが、やはり苦手とする受験生は多いですね。
例題はこんな感じ。

「入試数学の掌握 各論実戦編」の概要
いよいよラストですが、各論実戦編の概要を説明します。
各論実戦編は以下の目次のように3つのテーマに分かれています。


テーマ6とテーマ7はざっくりいうと図形に関する問題を扱っています。テーマ8は「与えられた誘導から出題者の意図を見抜く」ことが主題です。
それぞれみていきます。
「Theme6 解析武器の選択」はすっぴん図形の扱い方を学ぶパート
まずは例題をご覧ください。

この問題は一見簡単そうに見えて、解くとなると実は難しいんですが、その理由は以下の点にあります。
- 辺の長さや角度が定められていない
- どの分野の問題として解くべきか示唆されてない
本文の中で、京大の問題にはこの2つの特徴を持つ問題が多いと書かれています。こういった問題を苦手とする受験生は多いのですが、この類の問題への具体的なアプローチ方法を詳しく解説している教材を本書以外に見たことがありません。
具体的なアプローチ方法は実際に本書を読んで確認してもらいたいですが、かなり具体的に書かれています。
以下の画像のような誤答例があるのも本書の特徴の1つです。なぜ減点となるのかが明確に説明されているので、これはかなり大きいですね。

「Theme7 ものさしの定め方」は問題を違う角度から見ることに焦点を当てている
Theme7は説明が難しいので、まずは例題を見てもらいたいと思います。

この問題に対して、「直行する直線を座標軸として考えろ」と言っています。実際の解答例は以下のような感じです。

別解として、素直にそのまま座標軸をとった場合の回答例も載っています。

実際にやってみるとわかりますが、別解の場合は計算がめんどくさくなります。
Theme7では図形の問題について見方を変えると計算が楽になったり、解きやすくなる場合とそのアプローチ方法を解説しています。
上記のように2通りの解き方で具体的に説明してくれているのでとてもわかりやすいですし、「なるほど!こっちの解き方のほうがいいな!」と納得感があるので身につきやすいですね。
「Theme8 誘導の意義を考える」は見えにくい誘導を意識させることに重点を置いている
数学の問題といえば「誘導」も注意しておかなければいけないことの1つですが、最難関校ともなるとその誘導に気づきにくい問題も少なくないです。
というか、意識しなければどの部分が誘導なのかわからず問題を解くことになります。
Theme8では気づきにくい「誘導」を分類しどうアプローチするのかをまとめてあります。
誘導は主に次の2つのパターンに分類される、と本文には書いてあります。
- 結果を利用する
- 方針を利用する
大半は①に分類され②の頻度は低いようです。
例題を見てみましょう。

この例題に対して、以下のようなアプローチ(鉄則)を紹介しています。

例題の(2)の解答を見るとこのTheme8の概要が理解できます。

(←コレが気づきにくい)と書いてありますが、ここで(1)と(2)が繋がっていることがわかります。多くの人はよくわからないと思いますが、そういう人こそ本書を使って勉強することをオススメします。
こういった問題に対処するべく、本書では以下の合言葉を使っています。
「(1)と(2)に関連性がないようなときほど意図的につながりを疑え!」
Theme8では一見すると誘導になっていない問題でも実はつながりがあることや、そういう問題へのアプローチ方法を詳しく説明しています。この章も他の受験生と差をつけるためには必須だと思うので数強の人はぜひ目を通して見てください。
どういう人にオススメか
本書は使う人をかなり選びますが、だいたい以下のような人が使うといいと思います。
- 東大、京大、阪大、東工大、医大を目指す人
- 上記の人の中でなかなか得点が伸びない人
ほんとコレだけですね。早慶理科大の上位学部の人もギリOKだと思います。
東大、京大、阪大の場合は文理は問わず適正度は高いと思いますが、主に理系向けだと考えたほうがいいです。私大文系の場合はまず必要ないでしょう。
どのタイミング(時期)で、どう使うべきか
使うタイミングが難しいですが、内容が内容だけにじっくり取り組めるだけの余裕を持って使ったほうがいいと思います。
タイミングとしては遅くても11月末くらいには取りかかれるようにしておきたいところですね。それより遅い時期だと中途半端になって余計に混乱するかもしれません。
過去問をやりつつ、苦手とする問題パターンを本書で1つずつ学習していくのがオススメです。
3冊まとめて一気にやるよりも、過去問と並行して使うのが良いと思います。「よし、このテーマの内容はほぼ完璧だな!」というように1つずつ積み重ねていくイメージで使いましょう。
まとめ
1つの教材シリーズにここまでの時間を割いて分析したのは初めてですが、分析してみてそれだけの価値があることがわかりました。
この本は講師こそ読むべき本だと思います。普段なんとなく教えているような部分も、言語化し分類しているのでとても勉強になりました。
最後に「入試数学の掌握」についてまとめておきます。
- 東大、京大、阪大、国公立医大などの難関校を目指す人が使う
- 東工大志望でも使ってOK
- 早慶理科大の上位学部志望ならギリOK
- 総論編の問題数は60題
- 各論練磨編の問題数は51題
- 各論実戦編の問題数は70題
- 練磨編、実戦編は東大、京大、阪大、国公立医学部に特に特化した内容
分析してみてわかったのは、この本に書かれていることはめちゃくちゃ納得感が大きかったです。というのも、対象となる学力が違えど私も同じようなことを生徒に対して教えているからです。
要するに「こういうときはこうする!」ってところですね。
本書のすごいところは東大、京大、阪大、国公立医学部レベルの問題でもそこまで落とし込んで解説しているところです。本書に書かれたことを身につければそういった最難関校でも合格率を高められることは間違い無いと思います。
(2024/04/25 13:27:02時点 Amazon調べ-詳細)
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。







