2016年度版スタンダード数学演習12AB、問題番号228の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だけではわかりにくい部分を数学が苦手な人にもわかるように平易な説明をしてあるので参考にしてみてください。
略解(別冊解答)では余弦定理を使う方法が書かれていますが、実はもう少し楽に解く方法があります。まずは略解に沿った解法から行きましょう。
(1)の解説
解答例

![]() として、三角形ACD、三角形ECD、三角形BCDのそれぞれにおいて考えると、
として、三角形ACD、三角形ECD、三角形BCDのそれぞれにおいて考えると、
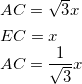
すると底面ABCは以下のような状態になる。
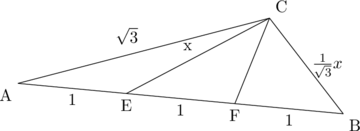
三角形ABCにおいて考えると、
(1) 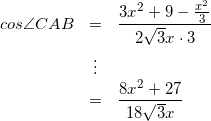
次に、三角形ACEについて考えると、
(2) 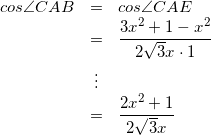
式(1)、(2)より
(3) 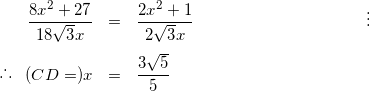
(1)のポイント
三角形ACEと三角形ABCはそれぞれ3つの辺をxと定数で表すことができている。また、![]() は共通の角である。つまり、それぞれの三角形で
は共通の角である。つまり、それぞれの三角形で ![]() の値を計算し連立すればxの方程式が作れるということになる。
の値を計算し連立すればxの方程式が作れるということになる。
ここがこの解法の最大のポイント。
余弦定理は3つの辺と1つの角の余弦、計4つの値に関する等式なので、そのうち2つがわからない場合は、その2つの値に関する式を2つ作って連立すれば求めることができる。
また、三角形ACEにおいて ![]() であることから
であることから ![]() になることに気づくかどうかもポイント。
になることに気づくかどうかもポイント。
(2)の解説
回答例
方針:![]() の形を目指す。
の形を目指す。

(まずはCFを求めに行く)
(4) 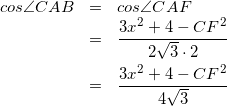
式(2)、(4)より、
(5) 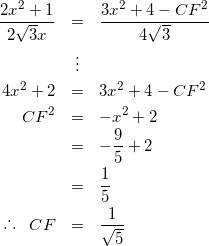
(次はDFを求めに行く)
(6) 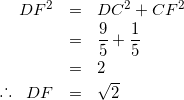
(最後に![]() に代入する。)
に代入する。)
(7) 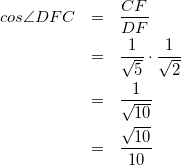
(2)のポイント
(2)のポイントは以下の点。
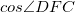 を求めろと言われているので関係ありそうな三角形CDFを取り出してみる
を求めろと言われているので関係ありそうな三角形CDFを取り出してみる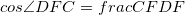 であることを利用する
であることを利用する
まずは基本動作ですが、関係ありそうな図形を取り出してみましょう。頭の中で考えるより圧倒的にわかりやすくなります。
![]() の値は余弦定理で求めてもいいですが、三角形CDFが直角三角形であることに気づけばより楽に解ける三角比の方を使えますね。
の値は余弦定理で求めてもいいですが、三角形CDFが直角三角形であることに気づけばより楽に解ける三角比の方を使えますね。
しかし、 ![]() を求めるには、先にDFとCFの値を求める必要がありそうです。DFかCFのどちらかが求まればもう一方は三平方や三角比を用いて求められます。
を求めるには、先にDFとCFの値を求める必要がありそうです。DFかCFのどちらかが求まればもう一方は三平方や三角比を用いて求められます。
別解
(1)の別解
(1)は中線定理でも解けます。![]() になってるところに反応して、中線定理を用いるんじゃないの?と思いつけるかどうかがポイントです。
になってるところに反応して、中線定理を用いるんじゃないの?と思いつけるかどうかがポイントです。

三角形CAFについて中線定理より、
(8) 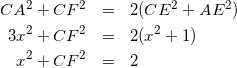
次に、三角形CEBについて中線定理より、
(9) 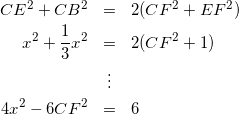
式(8)、(9)より、
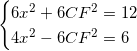
これを解いて、
(10) 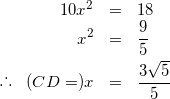
(2)の別解
(2)は式(8)と式(10)を用いると簡単に求められます。
式(8)と式(10)より、
(11) 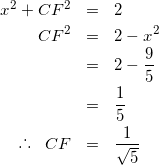
以降は同じです。
こっちの方が楽に解けるので図形と計量の問題というよりは図形の性質の問題に組み込んだ方がいいかもしれませんね。中線定理を使う問題は少ないのであえて図形と計量に分類してるのかもしれませんが。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。


