スタンダード数学演習12AB(2018)、「ベクトルと平面図形(1)」のA問題325の解説です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。
回答例の「方針」や( )内の説明は実際の回答ではないですが、解説のために入れてあります。
(1)の回答例
方針:とりあえず「言われた通り![]() を計算してみる」と「絶対値きたら2乗する」というセオリー通りやればOK。
を計算してみる」と「絶対値きたら2乗する」というセオリー通りやればOK。
((1)は図を描かなくても解けるので、そのままいきます。)
(1) 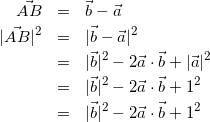
(![]() と
と![]() の値が必要ということがわかったので、次はそれらの値を求めにいきましょう)
の値が必要ということがわかったので、次はそれらの値を求めにいきましょう)
(2) 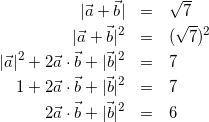
(3) 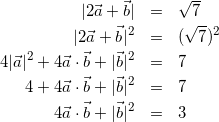
式(2)ー式(3)より
(4) 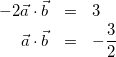
式(4)を式(2)に代入して
(5) 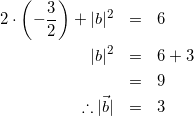
よって、式(1)より
(6) 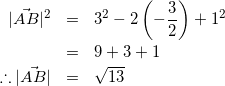
(2)の回答例
方針:(1)からABの大きさは一定。底辺の大きさが一定の三角形の面積が最大になるのは「高さが最大になるとき」に気づけば進めるはず。
(まずは図を書きましょう。以下、図を書くまでの説明が長くなりますが、必要な思考順序なので省略せず書きます。個人的には記述でも書いた方が良いと思いますがやや冗長かも。)
外接円の中心をI、Pから線分ABに下ろした垂線の足をHとすると、高さが最大となるのはHがABの中点になるとき。さらに高さが最大となるのは点Pが円の中心に関してABと反対側にあるときなので、点A、点B、点Pの位置関係は以下の図のようになる。
また、点Oについての位置は候補が2つあるが、(1)の結果を利用して位置は特定できる。
(1)より
(7) 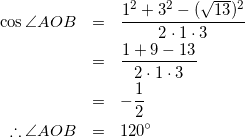
よって、点Oの位置は線分ABに関して常に点Iと反対側であることがわかる。以上より図は以下のようになる。
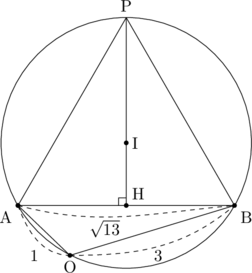
Hが線分ABの中点であり、線分PHと線分ABが垂直に交わることから、△PABはAP=BPの二等辺三角形。
さらに、円に内接する四角形の対角の和=180°なので
(8) 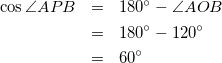
△PABの面積は
(9) 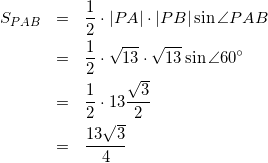
(3)の回答例
方針:(2)と同じように考えて、△QABの面積が最大となるのはQが点Oに関して線分ABと反対側にあるとき、ということを踏まえて図を書く。
(点Iを中心とする円は邪魔なので消しました。)
△QABの面積が最大となるとき、点Qの位置は下の図のようになる。また、点Qから線分ABに下ろした垂線の足をhとする。
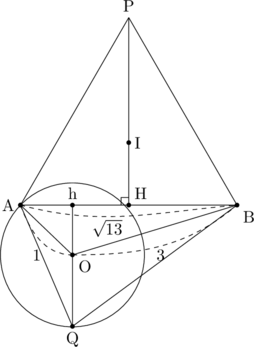
(△QABの面積は、Qhの長さがわかれば、底辺を線分ABとした三角形の面積として求められるので・・・)
![]() とおくと
とおくと![]() 。このとき、線分Ohの大きさについて2つの式が作れる。
。このとき、線分Ohの大きさについて2つの式が作れる。
△OAhについて見ると
(10) 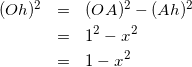
△OBhについて見ると
(11) 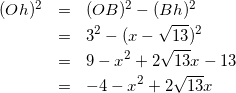
式(10)と式(11)より
(12) 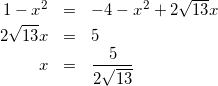
式(12)を式(10)に代入して
(13) 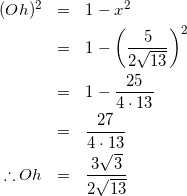
よって
(14) 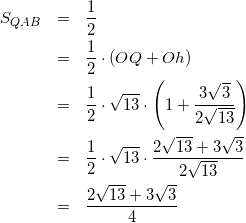
(1)のポイント
これはセオリー通りやるだけなのでそこまで難しいことはないと思います。
![]() のうちどの2つの組み合わせで計算してもOKです。
のうちどの2つの組み合わせで計算してもOKです。
例えば![]() を計算すると少しだけ速く
を計算すると少しだけ速く![]() を求められます。
を求められます。
(2)のポイント
(1)の結果を受けて、![]() を計算してみよう、と思えるかどうかがポイントですね。ここが回答の糸口です。
を計算してみよう、と思えるかどうかがポイントですね。ここが回答の糸口です。
これをやると点Oの位置が決まると同時に![]() の値もわかるので、一気に時進められるようになります。
の値もわかるので、一気に時進められるようになります。
ベクトルを使って求めることもできそうですが、平面図形の知識でといた方が早そうです。
ちなみに![]() の値は
の値は![]() で計算してもいいですが、コストは同じくらいでしょう。
で計算してもいいですが、コストは同じくらいでしょう。
(3)のポイント
Qh=OQ+Qh=1+Qhであることに気づくかどうかがポイント。Ohが円の半径でもあるのでOh=1であることに気づくかもポイントですね。
そうするとOhの大きさは△OABから求められそうなのはすぐにわかると思います。式(10)と式(11)を連立する方法は中学生で習いますね。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

