スタンダード数学演習12AB(2018)、「ベクトルと平面図形(1)」のA問題324の解説です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。
回答例の「方針」や( )内の説明は実際の回答ではないですが、解説のために入れてあります。
(1)の回答例
方針:相似の利用を考える。
(まずは図を書きましょう。わかりやすくするため△ABCと内心円だけ書きます。)
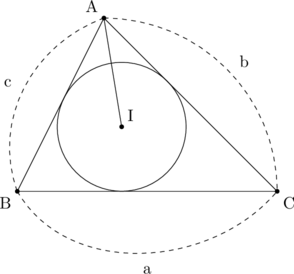
(問題文をそのまま図に表すと上のような図になります。ここに少し手を加えて、相似を利用できるようにします。)
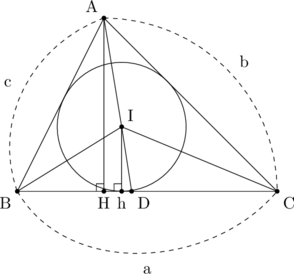
Aから線分BCに下ろした足をH、Iから線分BCに下ろした足をh、直線AIと線分BCの交点をDとする。
このとき、Ihは内心円の半径なので、2通りの方法で△ABCの面積を表すと、
(1) ![]()
(2) ![]()
式(1)と式(2)より
(3) 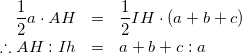
式(3)と△ADH∽△IDhであることから
(4) 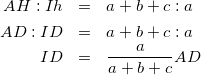
(AI=AD-IDに気づけば・・・)
(5) 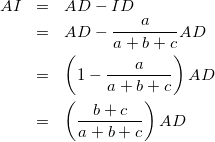
よって
(6) ![]()
ここで、Iが内心であることから線分ADは角BACの二等分線である。したがって
(7) 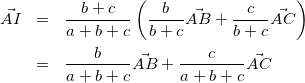
(2)の回答例
方針:この問題でセオリーとしてまず思いつくのは![]() の式を2つ作って係数比較なんですが、良い感じの式の作り方が見当たらないので、他のセオリーを考えます。
の式を2つ作って係数比較なんですが、良い感じの式の作り方が見当たらないので、他のセオリーを考えます。
(他のセオリーとしては、「内積を取ってみる」というのがあるので色々試してみましょう。)
(8) ![]()
(![]() と
と![]() の値が必要です。どちらも基本的な知識で求められそうです。)
の値が必要です。どちらも基本的な知識で求められそうです。)
![]() は外接円の半径なので、△ABCに対して正弦定理を用いて
は外接円の半径なので、△ABCに対して正弦定理を用いて
(9) 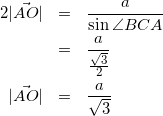
また、△ABOに余弦定理を用いて
(10) 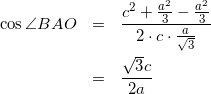
式(9)と式(10)を、式(8)に代入して
(11) 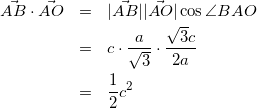
(ここで、![]() を他の方法で計算して、上の式と連立することを考えます。せっかくなので与えられた式、
を他の方法で計算して、上の式と連立することを考えます。せっかくなので与えられた式、![]() を使いましょう。)
を使いましょう。)
(12) 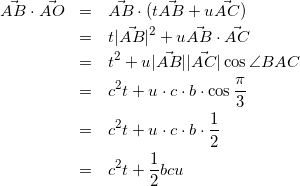
式(11)と式(12)より
(13) 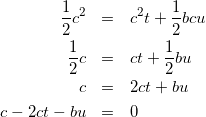
(同様に![]() も計算していきます)
も計算していきます)
(14) ![]()
(![]() の値はすでに求めてあるので、あとは
の値はすでに求めてあるので、あとは![]() の値が必要です。)
の値が必要です。)
△ACOに余弦定理を用いて
(15) 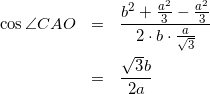
式(9)と式(15)を、式(14)に代入して
(16) 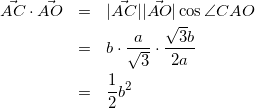
(![]() を他の方法で計算して、上の式と連立することを考えます)
を他の方法で計算して、上の式と連立することを考えます)
(17) 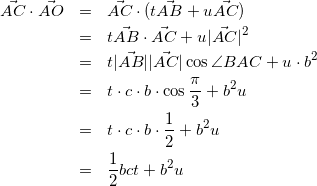
式(16)と式(17)より
(18) 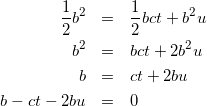
式(13)ー式(18)×2より
(19) 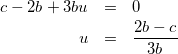
式(19)を式(13)に代入して
(20) 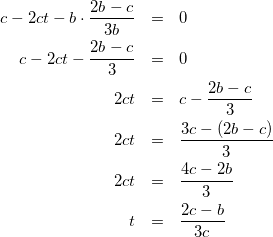
(1)のポイント
私は解答集を持っていないのでわかりませんが、もしかしたら回答例以外に簡単に解く方法があるかもしれません。
回答例のポイントは、三角形とそれに内接する円の場合、「式(4)のような比がわかる」ということです。
各辺の長さはa,b,cと変数で表されているので、この式(4)は一般的に成り立つということです。
回答例の解き方だとこれを知っているかどうかで大きな差が出ます。
結果を知っていれば、それを目指して式を作っていくことができますからね。何も知らないとそれすらできない。
この問題だけに限らず、「一般的に成り立つ式」は勉強しながらどんどん補充していくように心がけましょう。
この式(4)は「三角形とそれに内接する円」というよく見る問題設定なので、覚えておくと便利かもしれません。ただし、これを公式のようにして使うのはNGだと思います。途中式を示さずに使うと減点されるかもしれません。
(2)のポイント
(2)は(1)よりも最初の一手を見つけるのが簡単かもしれません。計算量も同じくらい。
![]() の値が与えられたので、その角を挟む辺であるAB、ACとAOの内積を考えるのが最も自然な流れですが、これをやろうと思いつくのは難しいかもしれません。
の値が与えられたので、その角を挟む辺であるAB、ACとAOの内積を考えるのが最も自然な流れですが、これをやろうと思いつくのは難しいかもしれません。
ここでも「とりあえず式を作ってみて、見通しを立てる」というセオリーが効いてきますね。
この回答例だと、式を作らずに「これだ!」という回答ルートを見つけるのは難しいと思います。
計算量が多いですが、![]() さえ計算できれば、
さえ計算できれば、![]() も同じようにして計算できるので後半は楽ですね。
も同じようにして計算できるので後半は楽ですね。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

