スタンダード数学演習12AB(2018)、「ベクトルと平面図形(1)」の基本問題109の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。
回答例の「方針」や( )内の説明は実際の回答ではないですが、解説のために入れてあります。
回答例
方針:三角形で面積といったらあの式ですよね。ベクトルの問題なので候補は2つありますが、どちらでもいいので式を書いてみましょう。
(この問題は図を描かなくても解きやすさに影響ないので図は描かなくてもOKです。とりあえず面積の式を。)
(1) 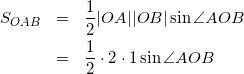
(ということで、![]() の値が必要なことがわかったので、次は
の値が必要なことがわかったので、次は![]() を求めましょう。)
を求めましょう。)
(2) 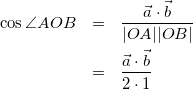
(こんどは![]() が必要です。まだ使ってない式があるのでそれを使うことを考えてみましょう。)
が必要です。まだ使ってない式があるのでそれを使うことを考えてみましょう。)
(3) 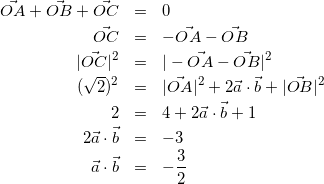
式(3)を式(2)に代入して
(4) 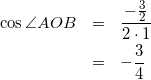
よって
(5) 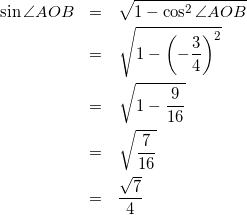
式(5)を式(1)に代入して
(6) 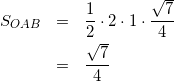
ポイント
とりあえず言われた通りにやってみる(この問題の場合は面積の式を作ってみる)のがセオリーですね。
式を作ってみると、次にやらなければいけないことが明確になるというのは数学の問題ではよくあることです。
三角形の面積の式ですが、回答例ではベクトルでの三角形の面積公式ではなく、三角比のところで出てくる公式を使っています。
三角比での三角形の面積の式
![]()
ベクトルでの三角形の面積の式
![]()
実はこの2つの式は内積の式を使えば全く同じものだということがわかります。試しにベクトルの方の三角形の面積の式に内積の式を代入してみましょう。
![]()
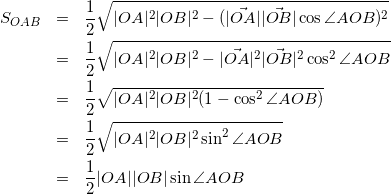
この式は三角比の場合の式と一致していますね。
参考書やテキストの解説の場合、式(3)から記述しはじめていることがよくありますが、これはやや不自然だと思います。
回答例のように「とりあえず面積を求める式を書いてみよう」→「sinの値が必要だ。sinを求めてみよう」→「内積が必要だ」と考えて行くのが自然な思考順序だと思います。
もちろん、これを頭の中で処理して式(3)からスタートしたり、よくわかんないけどとりあえず計算してみようと思って式(3)からスタートすることはあるかもしれません。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

