スタンダード数学演習12AB-2018

スタンダード数学演習12AB（2018）の解説　108

  /
2018スタンダード数学演習12AB

スタンダード数学演習12AB（2018）、「ベクトルと平面図形（１）」の基本問題108の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。

回答例の「方針」や（ ）内の説明は実際の回答ではないですが、解説のために入れてあります。

 

回答例

方針：セオリー通りでOK。点Pと点Qが一致することは２つの点の位置ベクトルが同じであることを示せば良い感じですね。

 

（とりあえず図を書きましょう。）

 

Rendered by QuickLaTeX.com

 

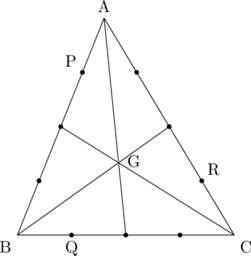
点A、点B、点Cの位置ベクトルをそれぞれ\vec{a}、\vec{b}、\vec{c}とする。また、△ABCの重心をGとし、その位置ベクトルを\vec{G}とすると

(1)   \begin{eqnarray*} \vec{G}&=&\frac{1}{3}(\vec{a}+\vec{b}+\vec{c})\\ \end{eqnarray*}

 

また、点P、点Q、点Rの位置ベクトルをそれぞれ\vec{P}、\vec{Q}、\vec{R}とすると

(2)   \begin{eqnarray*} \vec{P}&=&\frac{3\vec{a}+\vec{b}}{4} \end{eqnarray*}

(3)   \begin{eqnarray*} \vec{Q}&=&\frac{3\vec{b}+\vec{c}}{4} \end{eqnarray*}

(4)   \begin{eqnarray*} \vec{R}&=&\frac{3\vec{c}+\vec{a}}{4} \end{eqnarray*}

 

△PQRの重心をgとし、その位置ベクトルを\vec{g}とすると

(5)   \begin{eqnarray*} \vec{g}&=&\frac{1}{3}(\vec{p}+\vec{q}+\vec{r})\\ &=&\frac{1}{3}(\frac{3\vec{a}+\vec{b}}{4}+\frac{3\vec{b}+\vec{c}}{4}+\frac{3\vec{c}+\vec{a}}{4})\\ &=&\frac{1}{3}\frac{3\vec{a}+\vec{b}+3\vec{b}+\vec{c}+3\vec{c}+\vec{a}}{4}\\ &=&\frac{1}{3}\frac{4\vec{a}+4\vec{b}+4\vec{c}}{4}\\ &=&\frac{1}{3}(\vec{a}+\vec{b}+\vec{c}) \end{eqnarray*}

 

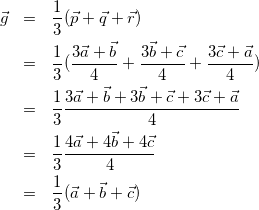
よって、式(1)と式(5)より△ABCと△PQRの重心は一致する。

 

ポイント

方針で示した通り、ベクトルの問題で２つの点が一致することはその２つの点の位置ベクトルが等しいことを示すのがセオリーですね。

重心のベクトルはいきなりポンっと書いてもOKだと思います。少なくとも模試で減点されたという例は見たことがないです。重心であることを宣言しておけば問題ないでしょう。

これは地味なポイントですが、\vec{G}と\vec{g}は重心を表すベクトルですが、異なるアルファベットで表記しておきましょう。例えば両方とも\vec{G}にすると、大幅に減点される可能性があります。

オンライン指導、生徒受付中！2月3月に指導開始の場合、割引！

神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。

  • 対象学年：中学生、高校生、浪人生
  • 指導科目（高校）：数学、物理、大学受験指導
  • 指導科目（中学）：数学、理科、高校受験指導
  • 指導形態：SkypeまたはZoomによるオンライン指導
  • 指導曜日・時間：要相談
  • 料金：1時間6,000円（税別）→5,000円（2月3月指導開始の方だけ！）
  • 体験指導：60分（ヒアリング含む）

 

体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

お問い合わせ

関連記事

COMMENT

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

CAPTCHA