スタンダード数学演習12AB(2018)、「ベクトルと内積」のA問題319の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。
回答例の「方針」や( )内の説明は実際の回答ではないですが、解説のために入れてあります。
(1)の回答例
方針:一見、設定がややこしいが、α、βを計算すると簡単になる。
(1) 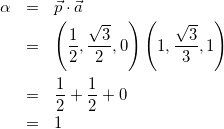
(2) 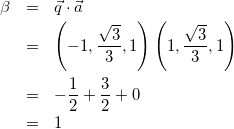
(3) 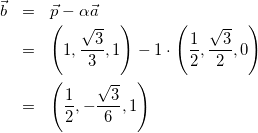
(![]() を計算するには
を計算するには![]() や
や![]() の値が必要なので、先に計算する。)
の値が必要なので、先に計算する。)
(4) 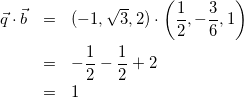
(5) 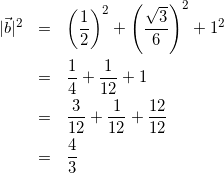
式(4)と式(5)より
(6) 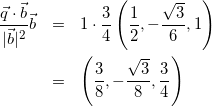
(7) 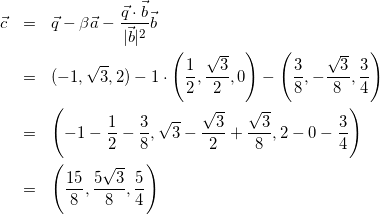
(2)の回答例
方針:O、A、B、Cの位置関係を知るために内積を計算してみる。
(8) 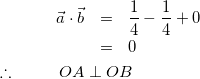
(9) 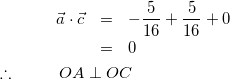
(10) 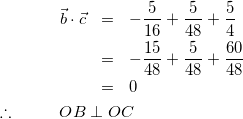
よって四面体OABCは次のような図になる。
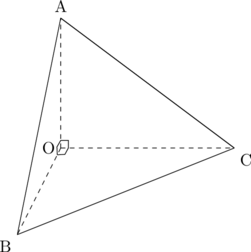
(OABCの体積は△OBCを底面、OAを高さとして計算したい。△OBCの面積を計算するのに![]() の値が必要なので先に計算する。)
の値が必要なので先に計算する。)
式(7)より
(11) 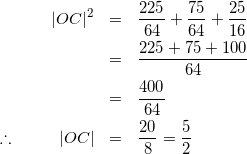
(12) 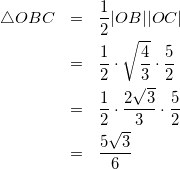
よって、OABCの体積は
(13) 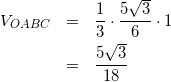
(1)のポイント
まずこの問題全体が「とりあえずなんかしら手を動かす」という習慣があるかどうかを試される問題。
問題文や与えられた条件を見て一般的なセオリーに結びつくようなわかりやすい情報はない。かろうじて「αやβは計算できそうだな」というところぐらいしか糸口がない。
αとβを計算すると芋づる式に計算できるようになるのが(1)最大のポイント。
(2)のポイント
(2)もとりあえず手を動かすことが重要だが、ベクトルの問題であることと(1)で![]() と
と![]() を成分表示させられたことがヒントになります。
を成分表示させられたことがヒントになります。
とは言え、この回答を思いつくのはかなり難しいのではないかと思いますね。
回答例以外にも座標の値から体積を求める方法もありそうです。めんどいからやってないけど。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

