スタンダード数学演習12AB(2018)、「ベクトルと内積」のA問題318の解説記事です。考えるときのポイント、式変形などを詳しく解説してあります。テキストの解説だとわかりにくい部分も細かく説明をしてあるので参考にしてみてください。
回答例の「方針」や( )内の説明は実際の回答ではないですが、解説のために入れてあります。
(1)の回答例
方針:kの値を求めるために![]() を式変形するところからスタート
を式変形するところからスタート
(1)の回答例はテキストに書いてあるものとは異なりますが、こちらの方がより自然な着想で解けていると思います。テキストの解説は別解として後述します。
(まずは図を書こう)
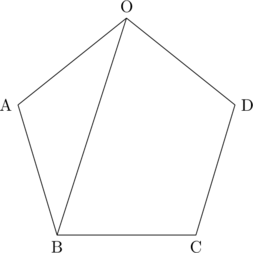
(1) 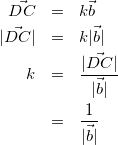
(kの値を求めるには![]() の値が必要。幾何的に解けそうなので図に手を加えていきます。)
の値が必要。幾何的に解けそうなので図に手を加えていきます。)
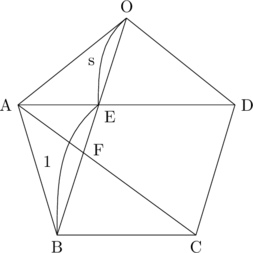
線分OBと線分AD、線分ACの交点をそれぞれE、Fとする。
線分OBと線分DC、線分ADと線分BCはそれぞれ平行なので、BE=CD=1。また、OE=sとすると、図形の対称性からBF=OE=1である。このことからEF=1-sとおける。
さらに図形の対称性から、AF=s、FC=1とおける。
△AFE∽△ACDより、
(2) 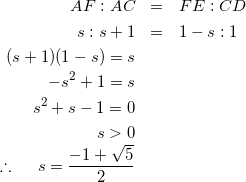
ここで、![]() なので
なので
(3) 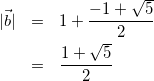
式(3)を式(1)に代入して
(4) 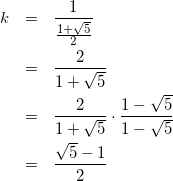
(kを求められたので、次は![]() を
を![]() 、
、![]() で表す方法を考えるが、セオリー通り、
で表す方法を考えるが、セオリー通り、![]() を扱いやすいベクトルに置き換える方向で考える。今の場合は題意
を扱いやすいベクトルに置き換える方向で考える。今の場合は題意![]() 、
、![]() に置き換えられそう。)
に置き換えられそう。)
![]() 同様に、図の対称性から
同様に、図の対称性から![]() なので
なので
(5) 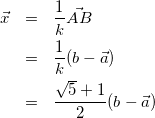
(図の対称性から考えて![]() も同様に考えればOK。今求めた
も同様に考えればOK。今求めた![]() も使えそう。)
も使えそう。)
![]() も同様に考えて
も同様に考えて
(6) 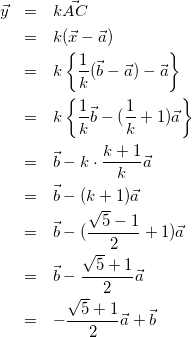
実はこの回答例は黄金比に関係あったりします。以下のように計算するとわかります。
(7) 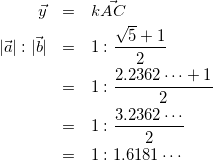
これは黄金比を求める有名な図形なので覚えておくと良いと思います。入試の問題はこういった有名な図形や問題をベースにした問題が出題されることがよくあります。
特に旧帝大や有名中学が入試問題で率先してそういった問題を作成し、他のところが易化コピーしていくことで広まります。広まった先では元々の題意が失われることはよくあることですね。
(2)の回答例
方針:内積の式からcosθ=の形に変形して見通しを立てる
(ベクトルでcosθの式といえば1つしかないのでそこから)
(8) ![]()
(![]() 、
、![]() というのはわかっているので、あとは
というのはわかっているので、あとは![]() の値が必要。(1)の結果を利用することを考える。)
の値が必要。(1)の結果を利用することを考える。)
(1)の結果から
(9) 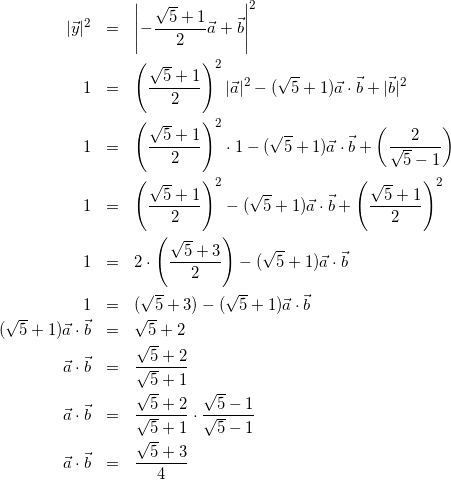
式(7)より
(10) 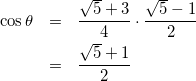
(3)の回答例
方針:内積の式にしたがって進める。また![]() と
と![]() のなす角が2θであることと(2)の結果を利用する。
のなす角が2θであることと(2)の結果を利用する。
(11) 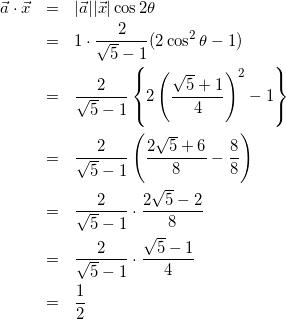
(1)のポイント
「kの求め方について」
入試の問題では正5角形や正6角形の問題はよく出題されます。一辺の長さがわかっていれば、対角線の長さも求められることを覚えておくと回答例のような解き方をすぐ思いつくことができるようになります。
また、正5角形の1つの対角線と向かい合う一辺は平行になります。この問題では![]() という条件を与えてくれてるので、証明なしでDCとOBは平行と言えるし、図形の対称性から他の線分の平行も無条件で使えます。
という条件を与えてくれてるので、証明なしでDCとOBは平行と言えるし、図形の対称性から他の線分の平行も無条件で使えます。
あとは相似を利用できそうだと気づけばkが求められることがわかります。相似については厳密には証明しないといけないかもしれませんが、OBとDCが平行な時点で自明なので回答例では省略しました。
「![]() と
と![]() について」
について」
![]() に気づくかどうかがポイントです。ここに気づくためには「扱いにくいベクトルは扱いやすいベクトルに置き換える」というセオリー通りに行動することが重要です。
に気づくかどうかがポイントです。ここに気づくためには「扱いにくいベクトルは扱いやすいベクトルに置き換える」というセオリー通りに行動することが重要です。
「![]() についても同様にすれば解けるな」というのは、同じように式を作ったときに
についても同様にすれば解けるな」というのは、同じように式を作ったときに![]() が出てくるのですぐに気づくと思います。なぜなら
が出てくるのですぐに気づくと思います。なぜなら![]() はこのときすでに求められていますからね。
はこのときすでに求められていますからね。
(2)のポイント
最初のとっかかりとしては内積の式を変形してcosθ=の形にするところから。
そのあと、![]() を求めるのが難しい。セオリーとしては「どうせ(1)の結果を使うんだろ」と考えて(1)の式を眺めて、2乗すれば
を求めるのが難しい。セオリーとしては「どうせ(1)の結果を使うんだろ」と考えて(1)の式を眺めて、2乗すれば![]() がうまく出現することに気付けるかどうかがポイント。
がうまく出現することに気付けるかどうかがポイント。
ベクトルの問題では「2乗する」というのはよく使うので覚えておこう。特に、どこかの内積が欲しいときに有効。
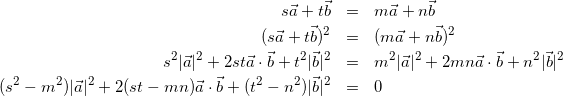
s,t,m,nはただの係数でなんでもいいです。重要なのはこういう計算をすると、![]() 、
、![]() 、
、![]() が出現するということを覚えておくことです。
が出現するということを覚えておくことです。
そうすれば、![]() や
や![]() の値さえわかれば
の値さえわかれば![]() が計算で求められるな、とわかります。
が計算で求められるな、とわかります。
この問題の場合はさらに、![]() を(1)で求めた値を使えば良いことはすぐにわかるはずです。
を(1)で求めた値を使えば良いことはすぐにわかるはずです。
(3)のポイント
方針でも書いたように、![]() と
と![]() のなす角が2θであることに気づくかが最初のポイントです。
のなす角が2θであることに気づくかが最初のポイントです。
式(10)の1行目さえ書ければ、cos2θを倍角の公式で変形すればいけるなと思えるはずです。思えない人はそもそも演習量が足りてないのでたくさん練習しましょう。
また思いついたけど倍角の公式を忘れた、導出できない、という人はおしいですね。おしいですが、やはり演習不足なので練習しておきましょう。
公式類は必ず覚えましょう。倍角などは加法定理から導出できますが、本番で導出している時間はないので、使いたい形でパッと書けるようにしておいたほうがいいですね。
(1)の別解
方針:どうにかして連立方程式に持ち込む。
(テキストの解答ヒントを参考に進めます)
△OABにおいて
(12) 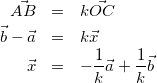
△OBCにおいて
(13) 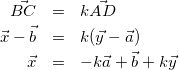
△OCDにおいて
(14) 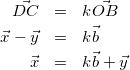
式(11)と式(12)より
(15) 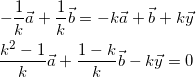
式(11)と式(13)より
(16) 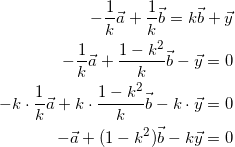
式(14)-式(15)より
(17) ![]()
![]() と
と![]() は平行ではないので、
は平行ではないので、![]() (tは実数)。よって、式(16)が成り立つ条件は
(tは実数)。よって、式(16)が成り立つ条件は![]() 、
、![]() それぞれの係数が0のとき。つまり、
それぞれの係数が0のとき。つまり、![]() かつ
かつ![]() のとき。
のとき。
(18) 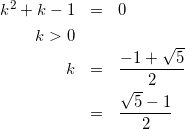
このとき![]() の値は
の値は
(19) 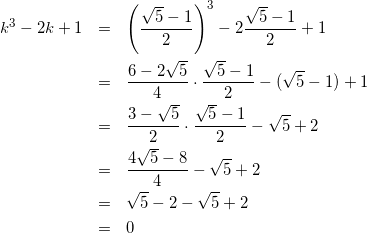
よって、![]()
(1)の別解のポイント
テキストの解答だとこの別解の最初がヒントとして書かれていますが、「式(11)〜式(13)を作ってみよう」と思う人はあまりいないような気がします。
思いついたとしてもその先の連立方程式がいまいちわかりにくい。
テキストの解答集を持っておらず実際の解答がどうなっているのかわからないのでなんとも言えないが、回答例にしろ別解にしろ難しい。
(1)さえ突破できれば満点できる問題なんですが、こういう問題はいまいちですね。もしこの問題の配点が30点なら、0点か30点の人が多くなりますからね。
(1)よりも(2)、(2)よりも(3)が難しいのが理想的です。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。

