2016年度版スタンダード数学演習12ABの346の解説です。2017年版以降を使っている人は問題が合っているかよく確認してください。
回答例
方針:与えられた条件からできる限り図を書いてみる。特に![]() の利用は重要
の利用は重要
![]() より
より
(1) 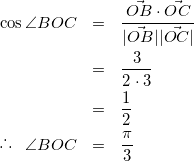
(これで、![]() の角度がわかりました。これと、
の角度がわかりました。これと、![]() 、
、![]() 、
、![]() という情報から、A、B、Cはそれぞれ下の図のような3つの円上のどこかにあることがわかります。)
という情報から、A、B、Cはそれぞれ下の図のような3つの円上のどこかにあることがわかります。)
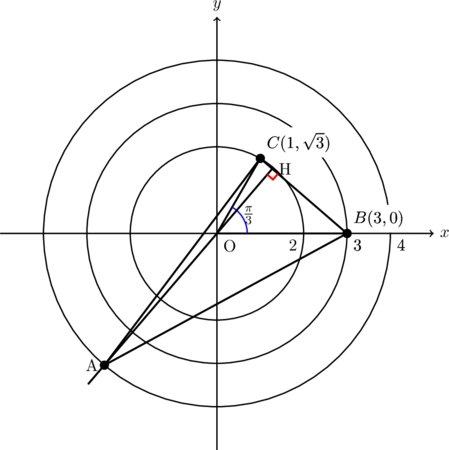
(ここからがこの問題の難しいところです。![]() は
は![]() で一定なので、点Bと点Cの相対的な位置関係は常に同じです。なので、点Bと点Cを上の図のように固定して考えればOKです。)
で一定なので、点Bと点Cの相対的な位置関係は常に同じです。なので、点Bと点Cを上の図のように固定して考えればOKです。)
(線分BCを底辺とし、点Aから線分BCに下ろした垂線を高さとみて考えましょう。まずは線分BCの長さから求めます。)
(2) 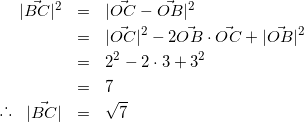
(つづいて線分AHを求めます。)
(3) ![]()
(OHについては三角形OBCに注目して考えます。)
![]() とおくと、三角形BOHと三角形COHについて三平方の定理を用いると、
とおくと、三角形BOHと三角形COHについて三平方の定理を用いると、
(4) 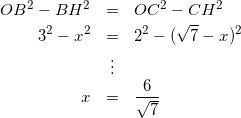
よって、
(5) 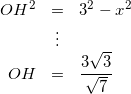
式(5)とOA=4を式(3)に代入して、
(6) 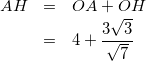
これで最大となるときの三角形ABCの面積を求める準備ができました。
(7) 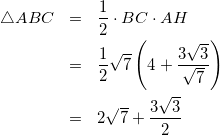
この問題のポイント
- 点Bと点Cの相対的な位置関係が変わらないことに気付けるかどうか
OBとOCのなす角が![]() と一定、OBもOCも一定なので辺BCの長さも一定の値になるはずです。
と一定、OBもOCも一定なので辺BCの長さも一定の値になるはずです。
このことから、三角形OBCを形を変えずに原点Oを中心に回転させるイメージを持てればOKです。
また、辺BCを底辺と見たとき、辺BCが一定であるなら三角形ABCの面積は高さによって決まるということに気付けるかどうかもポイント。
検討
点Bと点Cの位置をそれぞれ、![]() 、
、![]() と固定して考えましたが、他の座標にあったらどうでしょうか。仮に点Bが
と固定して考えましたが、他の座標にあったらどうでしょうか。仮に点Bが![]() (つまり反時計回りに90°回転した場所)にある場合を考えてみます。図はこんな感じになるはずです。点Cの座標は自分で求めてみてください。
(つまり反時計回りに90°回転した場所)にある場合を考えてみます。図はこんな感じになるはずです。点Cの座標は自分で求めてみてください。
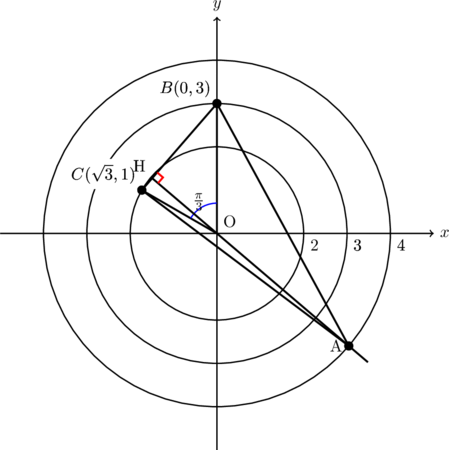
元の図形を反時計回りに90°回転させたでけというのがわかりますね。何°回転させても同じことが言えるので、最初の位置で固定して考えても差し支えないはずです。
また、最初の位置から線対称に移動させた場合でも同様で、元の図形と合同な図形になります。
このことに気づけば点Bと点Cは![]() という値と、それぞれの円周上にあるという条件を満たしていればどこにあってもいいことがわかります。
という値と、それぞれの円周上にあるという条件を満たしていればどこにあってもいいことがわかります。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年:中学生、高校生、浪人生
- 指導科目(高校):数学、物理、大学受験指導
- 指導科目(中学):数学、理科、高校受験指導
- 指導形態:SkypeまたはZoomによるオンライン指導
- 指導曜日・時間:要相談
- 料金:1時間6,000円(税別)→5,000円(2月3月指導開始の方だけ!)
- 体験指導:60分(ヒアリング含む)
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。


