2019年（平成31年度）の都立高校入試の筆記試験が終わりましたね。数学の難易度は例年通りだったと思います。この記事では比較的難しかった第3問の問2の②、第4問の問2、第5問の問2の解説をしたいと思います。また、各問題の難易度も評価してみました。
問題と回答は以下のリンクをご覧ください。
各問題の難易度
問題の難易度を5段階で評価してみました。
- 第1問：問1★☆☆☆☆、問2★☆☆☆☆、問3★☆☆☆☆、問4★☆☆☆☆、問5★☆☆☆☆、問6★☆☆☆☆、問7★☆☆☆☆、問8★☆☆☆☆、問9★☆☆☆☆
- 第2問：問1★★★☆☆、問2★★★☆☆
- 第3問：問1★★☆☆☆、問2・①★★☆☆☆、問2・②★★★★☆
- 第4問：問1★★★☆☆、問2・①★★★☆☆、問2・②★★★★★
- 第5問：問1★★★☆☆、問2★★★★☆
第1問は計算と各単元の基本問題。作図も基本的なものなので正答率は高そうです。
第2問はどちらも標準レベルの空間図形&文字式に関する問題。苦手な人が多いところなので難易度は3としました。
第4問の問2・②が最難関だったと思います。正答率もかなり低いと思われます。
第3問〜第5問は比較的難しい問題が多いので例年苦戦する人が多いところですが、例年通り各大問のラストの問題以外をどれだけ取れるかの勝負だったかなと。
以下で比較的難しかった問題のみ解説していきます。
第3問、問2の②の解説
この問題は答えを出すまでの道のりが長いので正答率が低かったのではないかと思います。数学の問題を解く上での基本スキル「何が欲しいのか考える」が身についている人は割と簡単に解けたと思いますが。
まずは回答方針を考えます。
最終的にはPの座標を求めたいのでまずはPのx座標をpと置くところからスタートですね。するとMのx座標もpとなります。未知数pを求めたいので何らかの方程式を作りたいわけですが、中点Mが直線OB上にあることから直線OBの式を求めて点Mの座標がその上にあることから方程式を作れば良さそうです。
ということで、まずは図を書いてPの座標をpで表してみます。
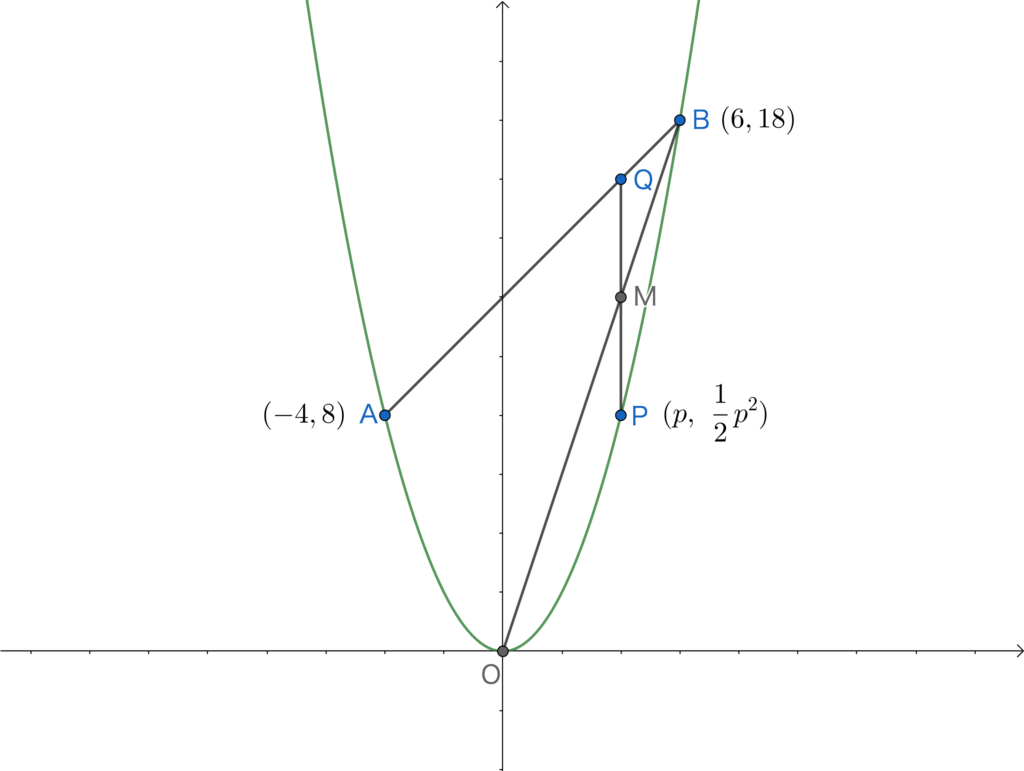
中点Mの座標をpで表すためには点Qの座標をpで表す必要があります。点Qのx座標もpであることから、直線ABの式を求めてその式にx=pを代入すれば点Qのy座標もpで表せそうです。
直線ABの傾きは、
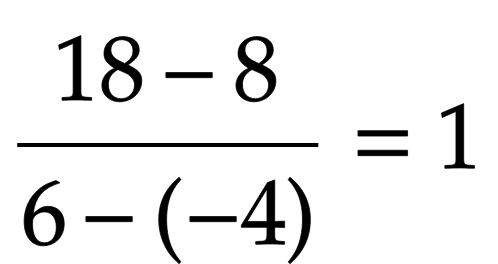
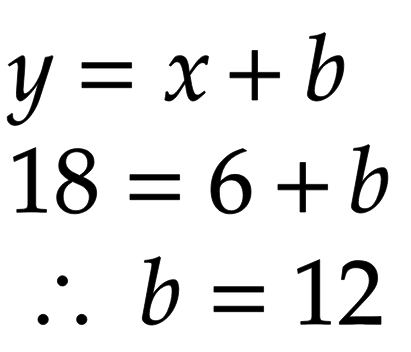
よって、直線ABの式は、
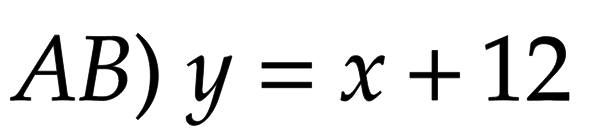
となる。この式に、x=pを代入して、
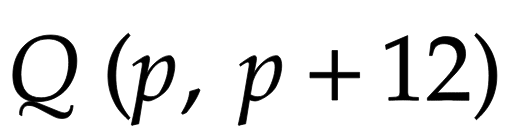
ここまでの情報をグラフに書き込んでおくと以下のようになります。
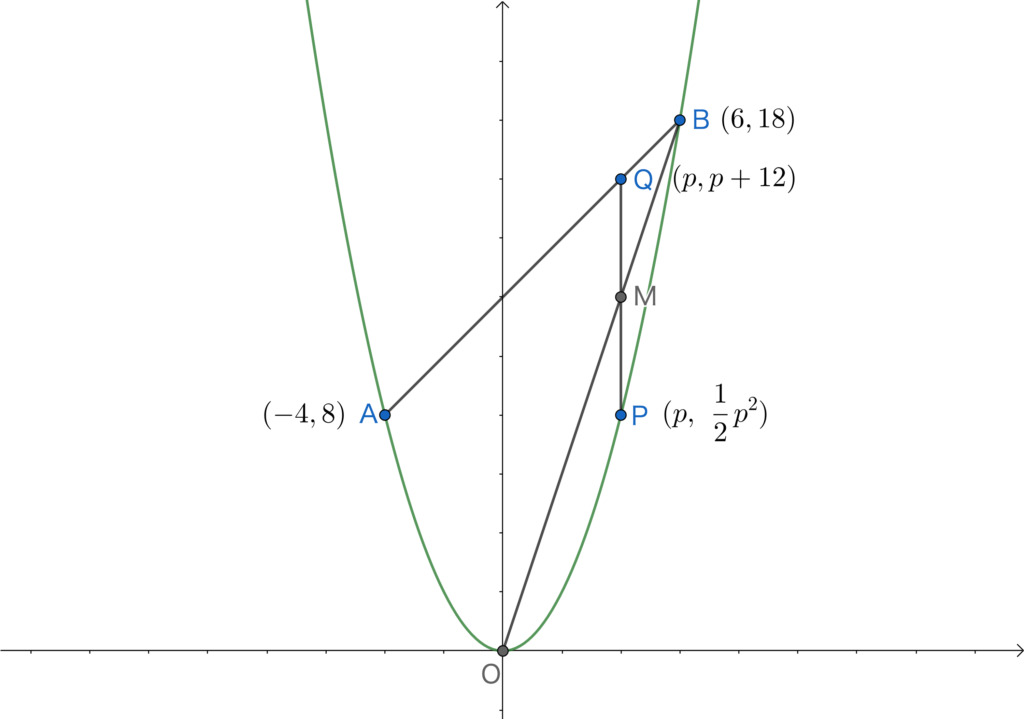
次に中点Mの座標をpで表します。x座標はp。y座標はPとQの中点として求めます。
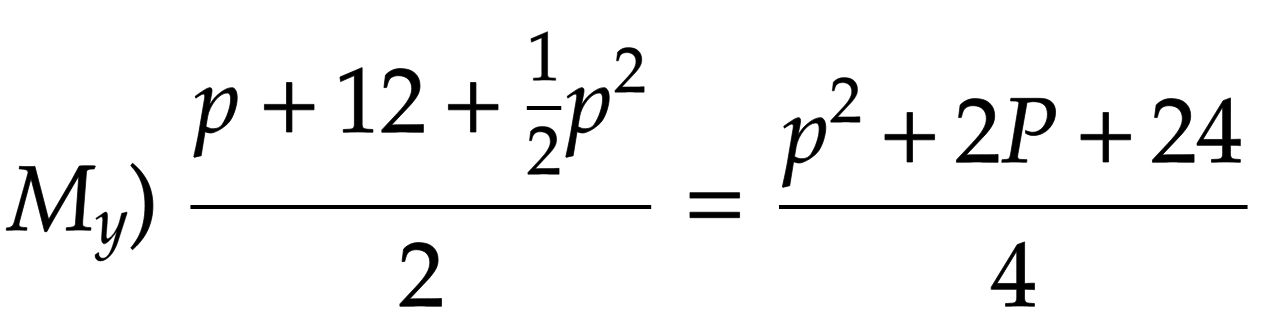
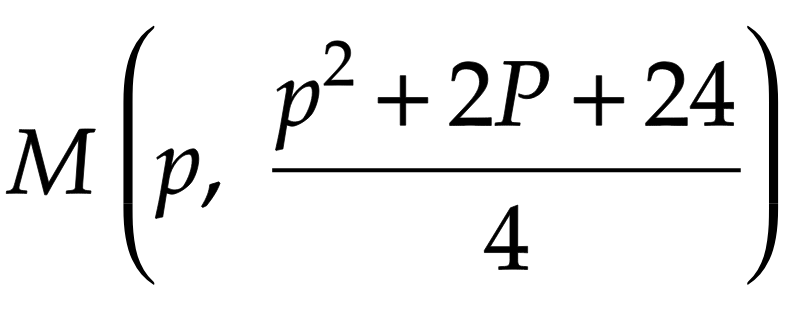
これが直線OB上にあるので、次に直線OBの式を求めます。直線OBは原点Oを通るのでy切片は0です。傾きは3なので、
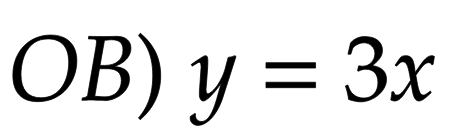
これに先ほど求めたMの座標を代入します。ここまでくれば解けそうだとわかる人も多いはず。
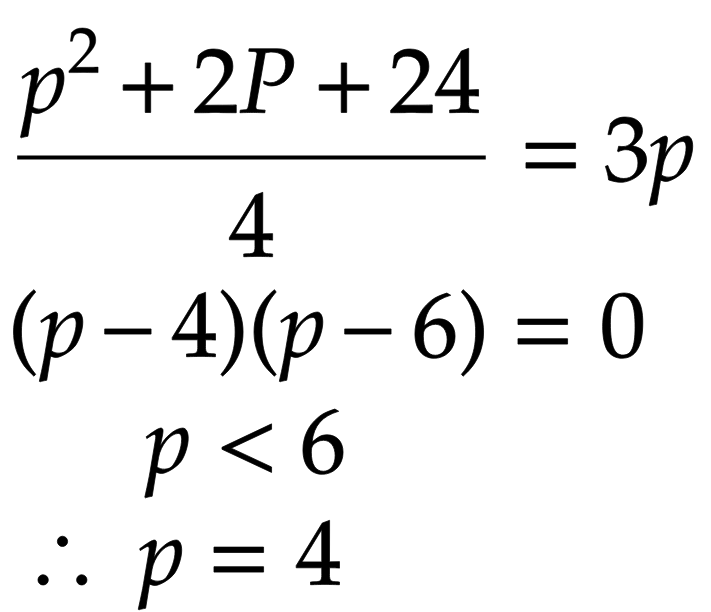
よって、pの座標は、
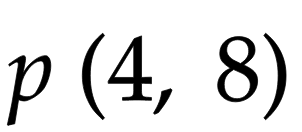
最初に書いた回答方針のようなことをいきなり思いつくのは難しいですが、問題文に「中点」と書かれた時点で「中点を求めに行く」という行動を取るのはセオリーですので反応できるようにしておきたいですね。
同様に、「求めたい値を適当な文字で置く」というのもセオリー中のセオリーです。特に函数の場合は、x座標を適当においてy座標もその文字で表す、という流れはよく出てきます。
ここまでやってみればその先の回答方針がわかる人もいるはず。
回答方針が立てられない場合でも、とりあえず「やれることをやる」「セオリー通りやってみる」ことでその先が見えてくることが多いですね。
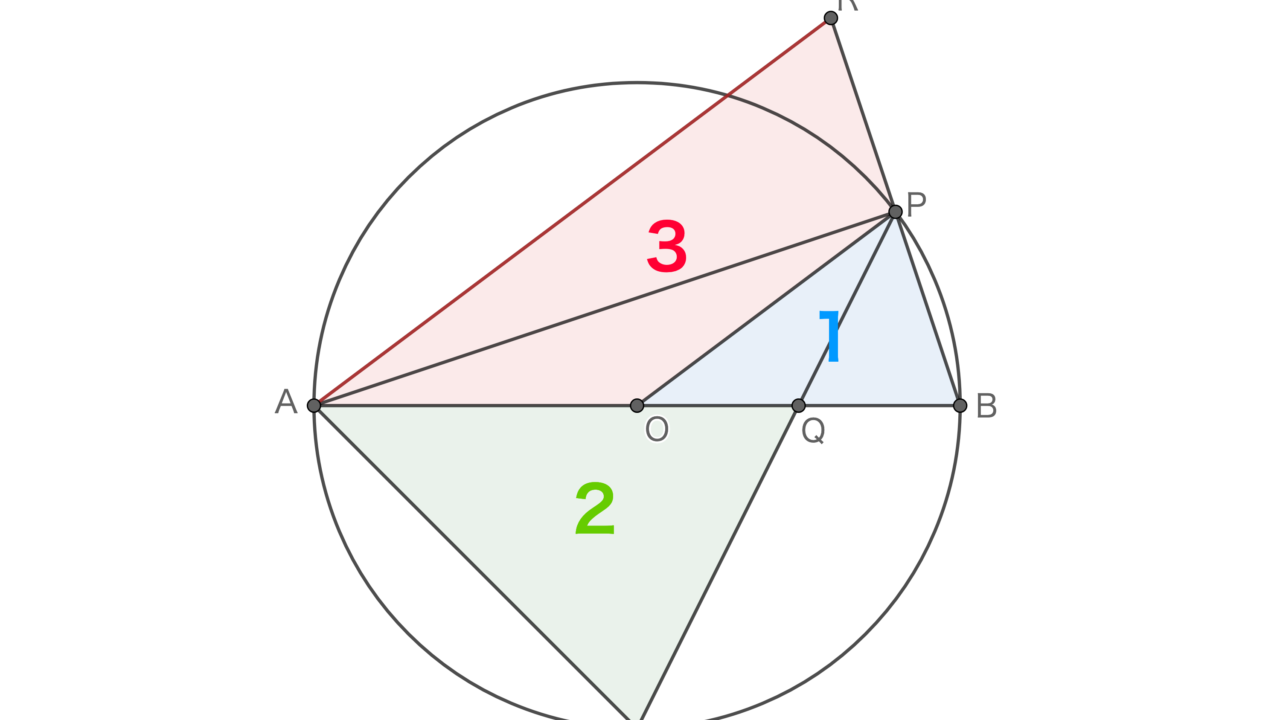
第4問の問2の解説
おそらくこの問題が一番難しかったはず。正答率も3%切ってそう。
この問題を解くためのポイントは以下の3つ。
- △OBP∽△ABRであることに気づくか
- △ACQ∽△OBPであることに気づくか
- △ACQと△OBPの相似比が√2:1であることがわかるか
１つずつ見ていきましょう。
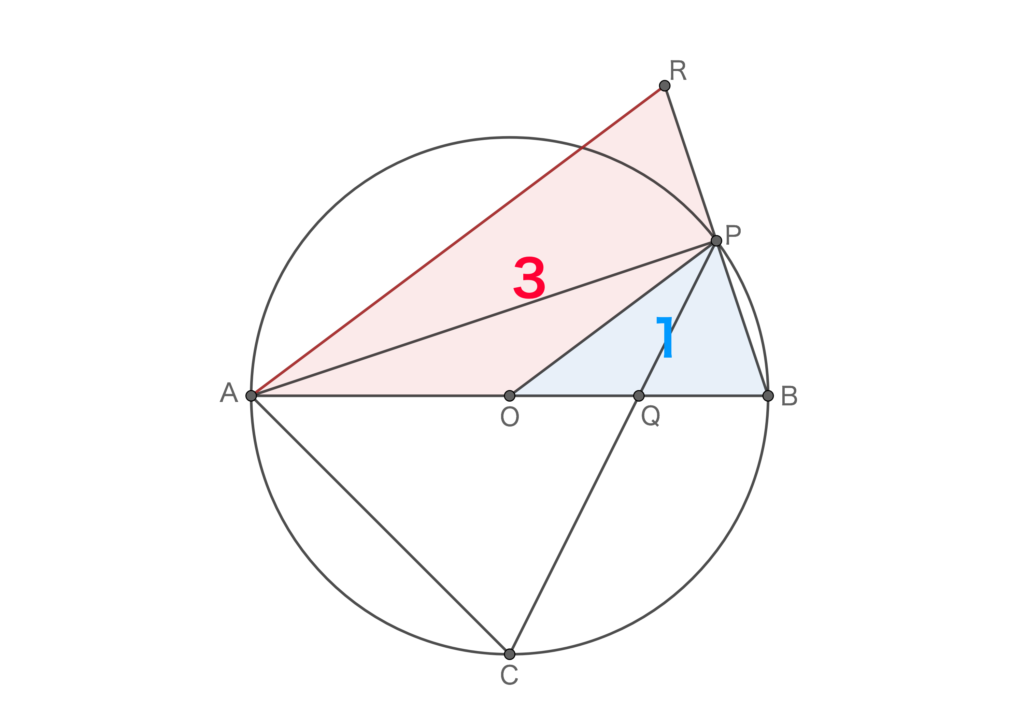
まず最初に□AOPRときてピンとくるところがあります。OとPはそれぞれ辺ABとBRの中点なので、中点連結定理より△OBP∽△ABRということがわかります。ここで、△OBPと△ABRの相似比が1:2であることから、△OBPと□AOPRの面積比は1:3とわかります。
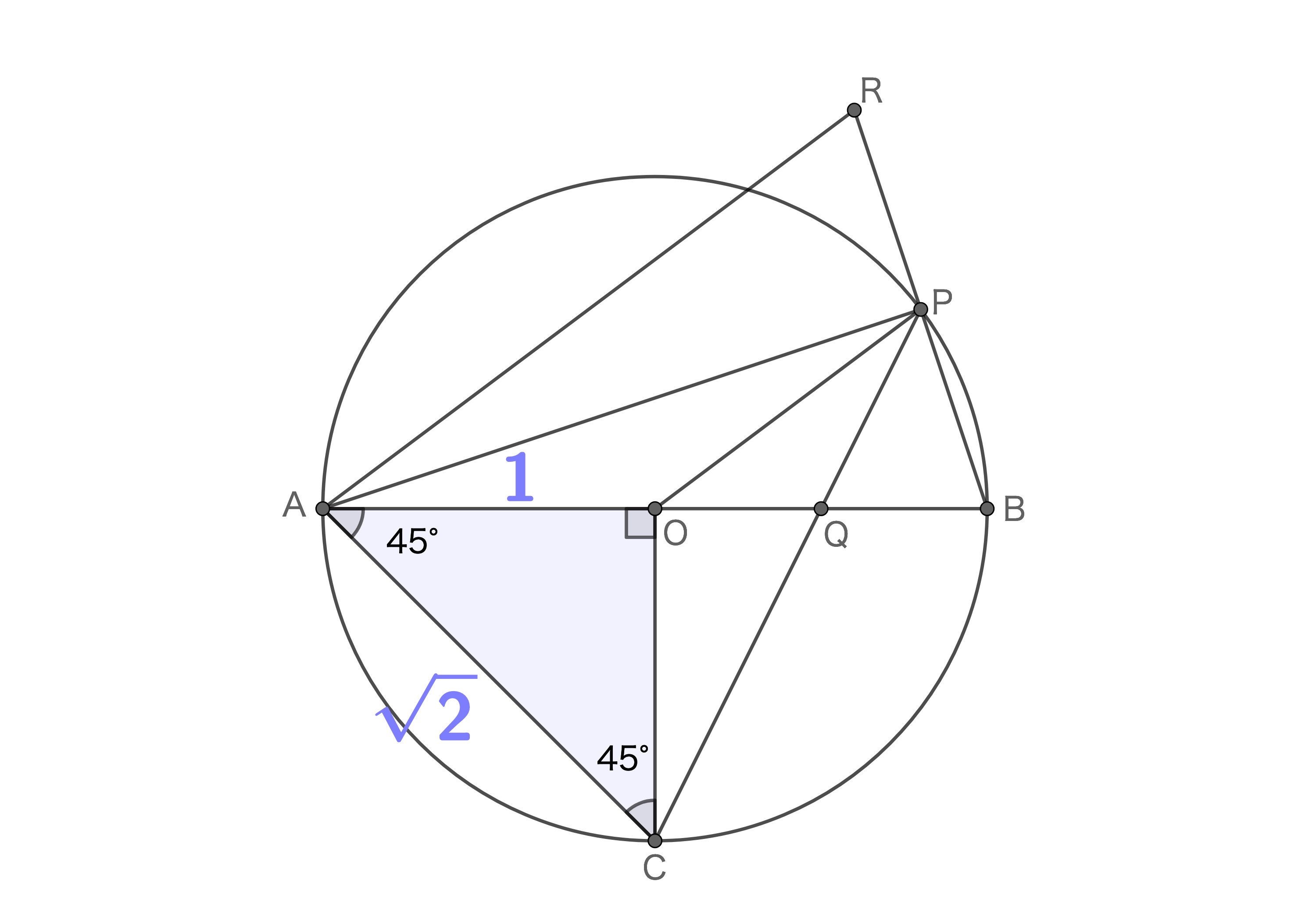
次に、弧BC=2×弧BPであることから角BAC=角BOPであることがわかります。また、弧APに対する円周角は等しいので角ACP=角ABP。よって、△ACQ∽△OBP。
ここからさらに難しいですが、Cが弧ABの中点であることから、△AOCは直角二等辺三角形であることがわかります。辺AOの長さを1とするとACの長さは√2です。一方、AO=BOなので、△ACQと△OBPの相似比は√2:1となり、面積比は2:1となります。
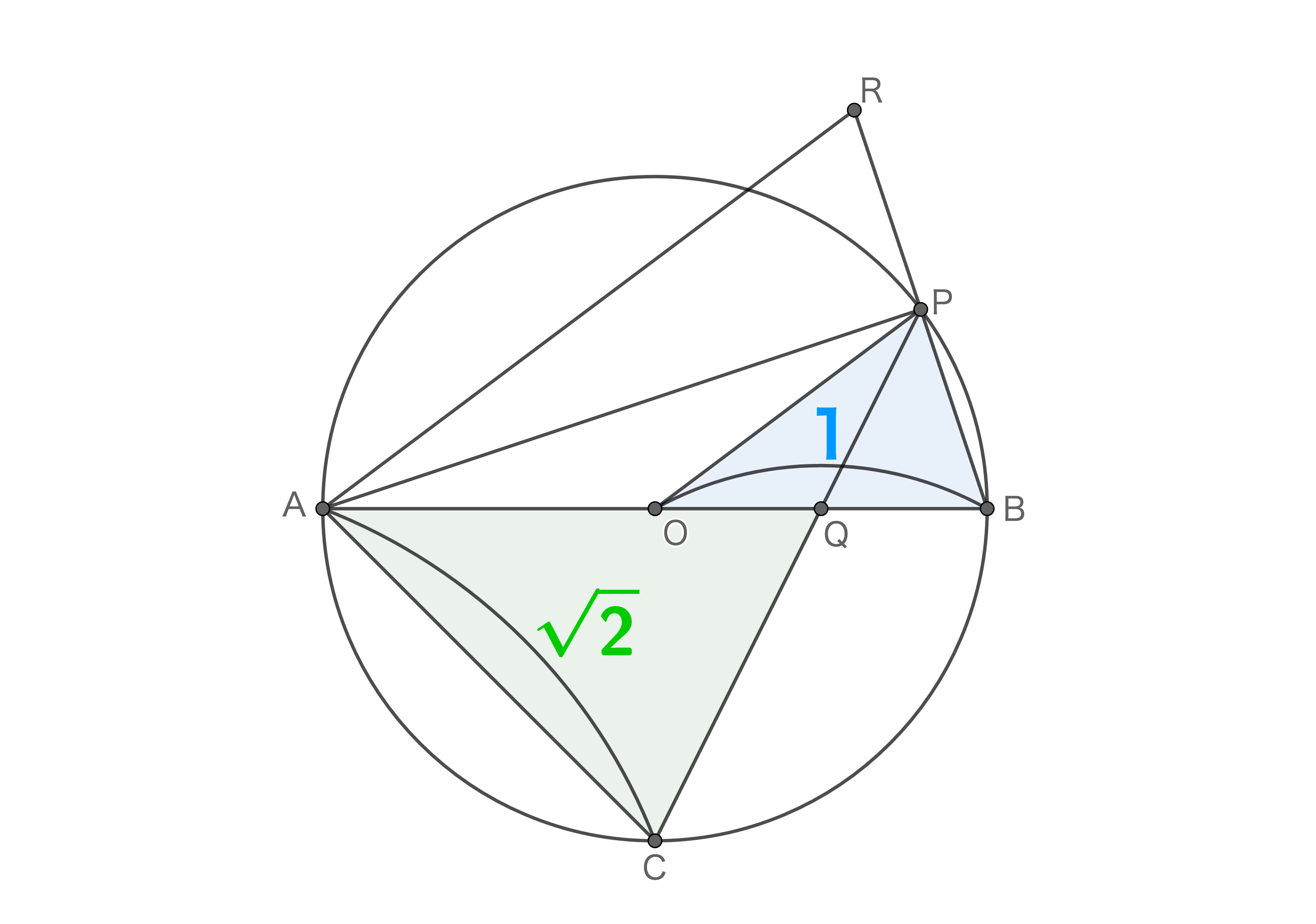
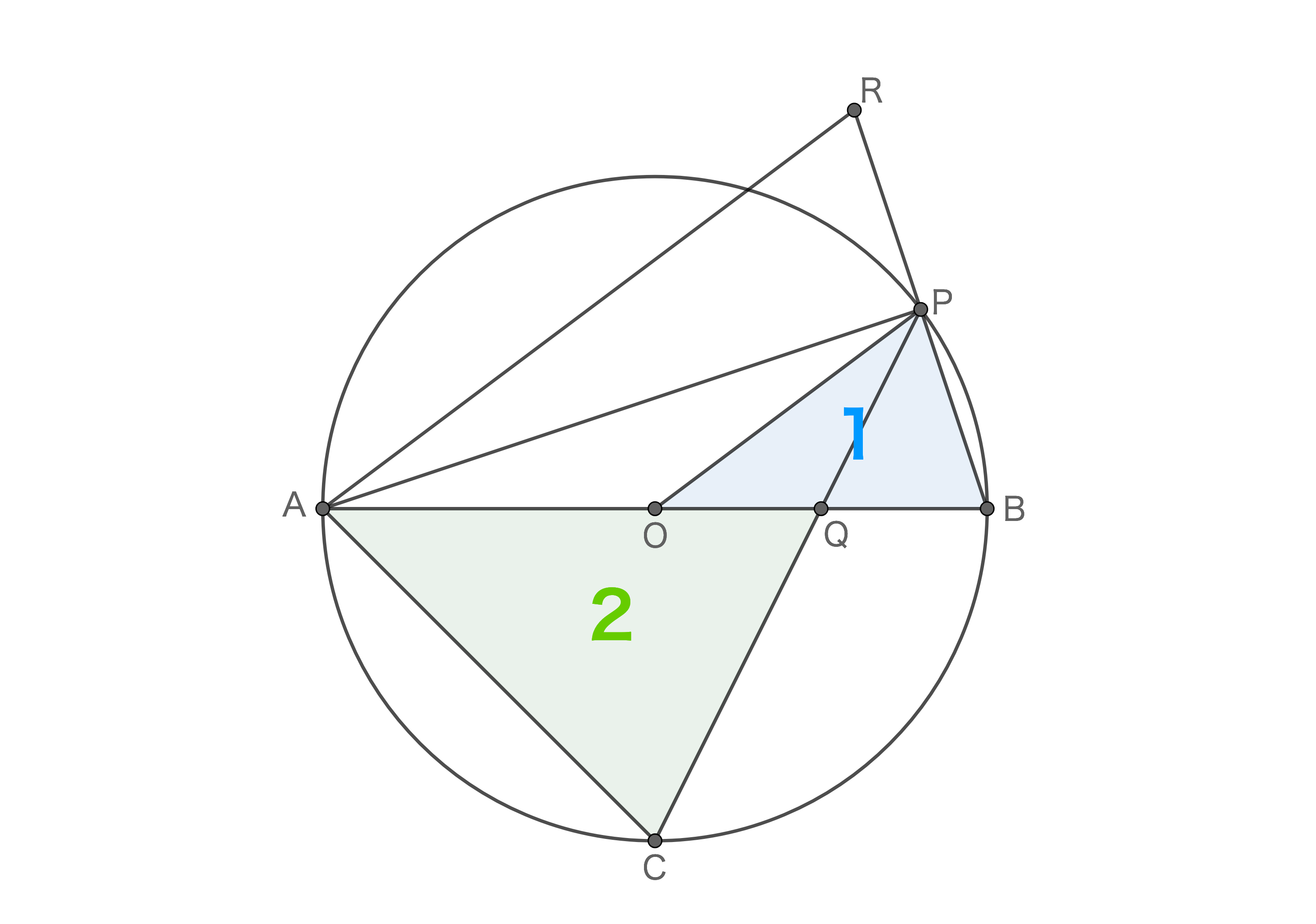
ここまでの面積比をまとめると△ACQ:△OBP:□AOPR=2:1:3となります（下図）。よって、△ACQの面積は□AOPRの2/3となります。
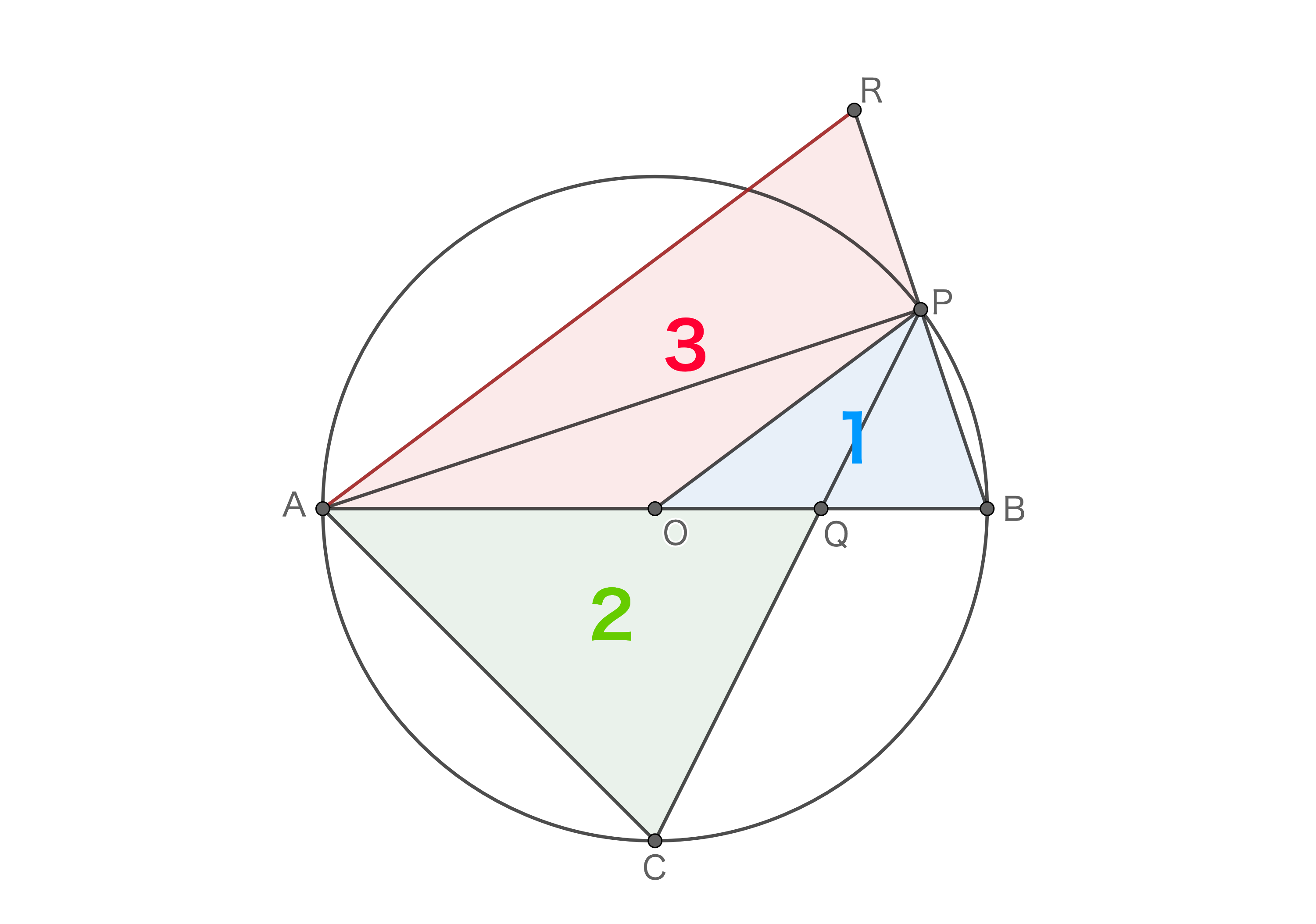
この問題は、中点連結定理を使うことや△AOCが直角二等辺三角形であることに気づきにくい問題文の書き方をしているので難易度が高いです。問題文に「中点」とか書いてあればすぐに反応できますが。まあでも、□AOPRっていう不自然な面積が問題になってるので、気づくかもしれないですね。
第5問の問2の解説
この問題のポイントは以下の2点。
- 高さをどこに取るか
- その高さをどこから見るか
パッと見で方針は2つありそうです。１つは体積を直接求めに行く方法。もう１つは全体から他の体積を引く方法。検討してみるとすぐにわかりますが後者は各体積の高さを求めるのに時間がかかりそうなので保留ですね。ということで前者の解き方でいきます。
図2を真上からみると以下のような図になります。
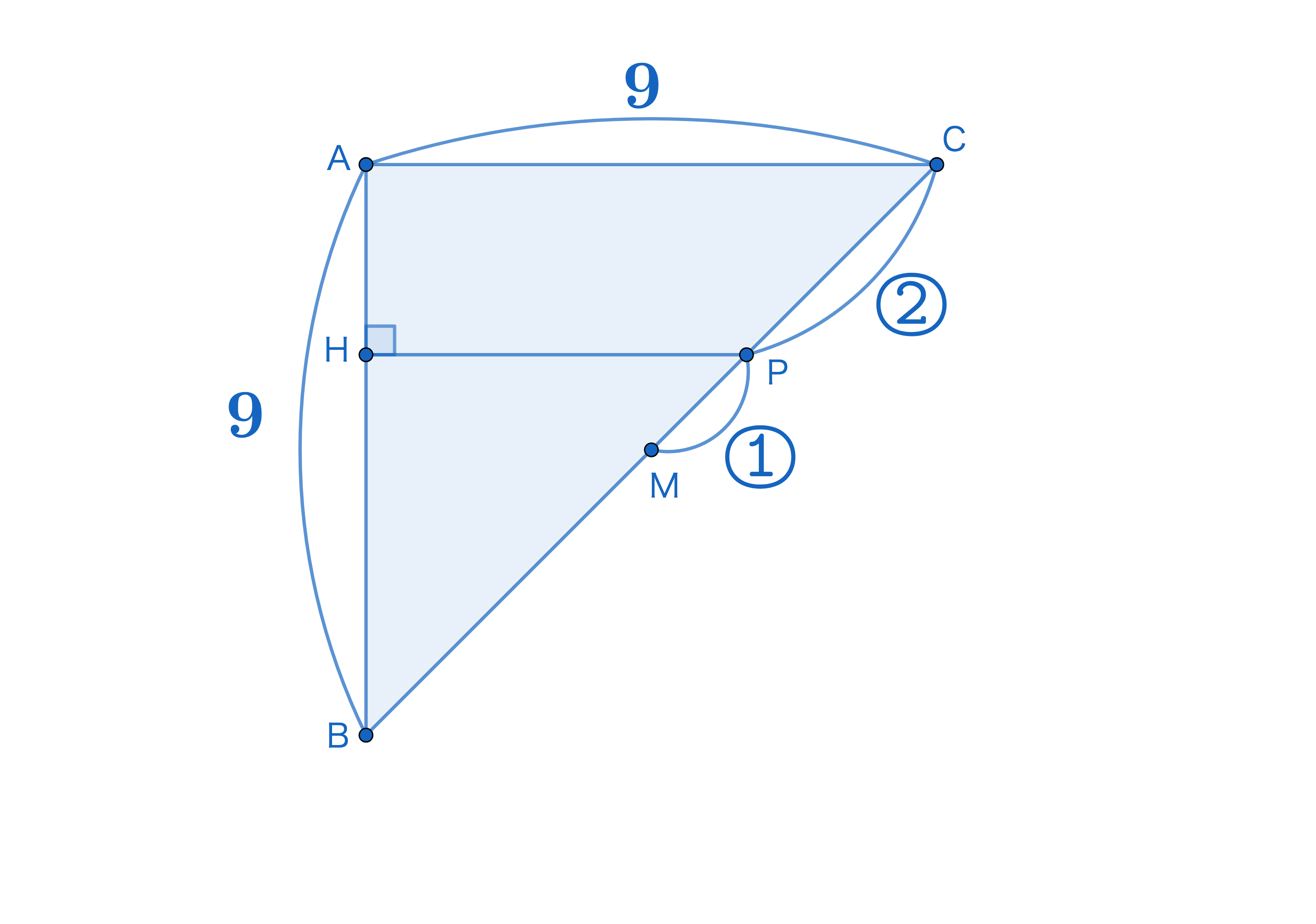図の性質を考えるとこの図のPHが求めたい体積の高さに相当することがわかります。ちなみに底面は△ABDです。あとは相似を利用してPHを求めればOK。
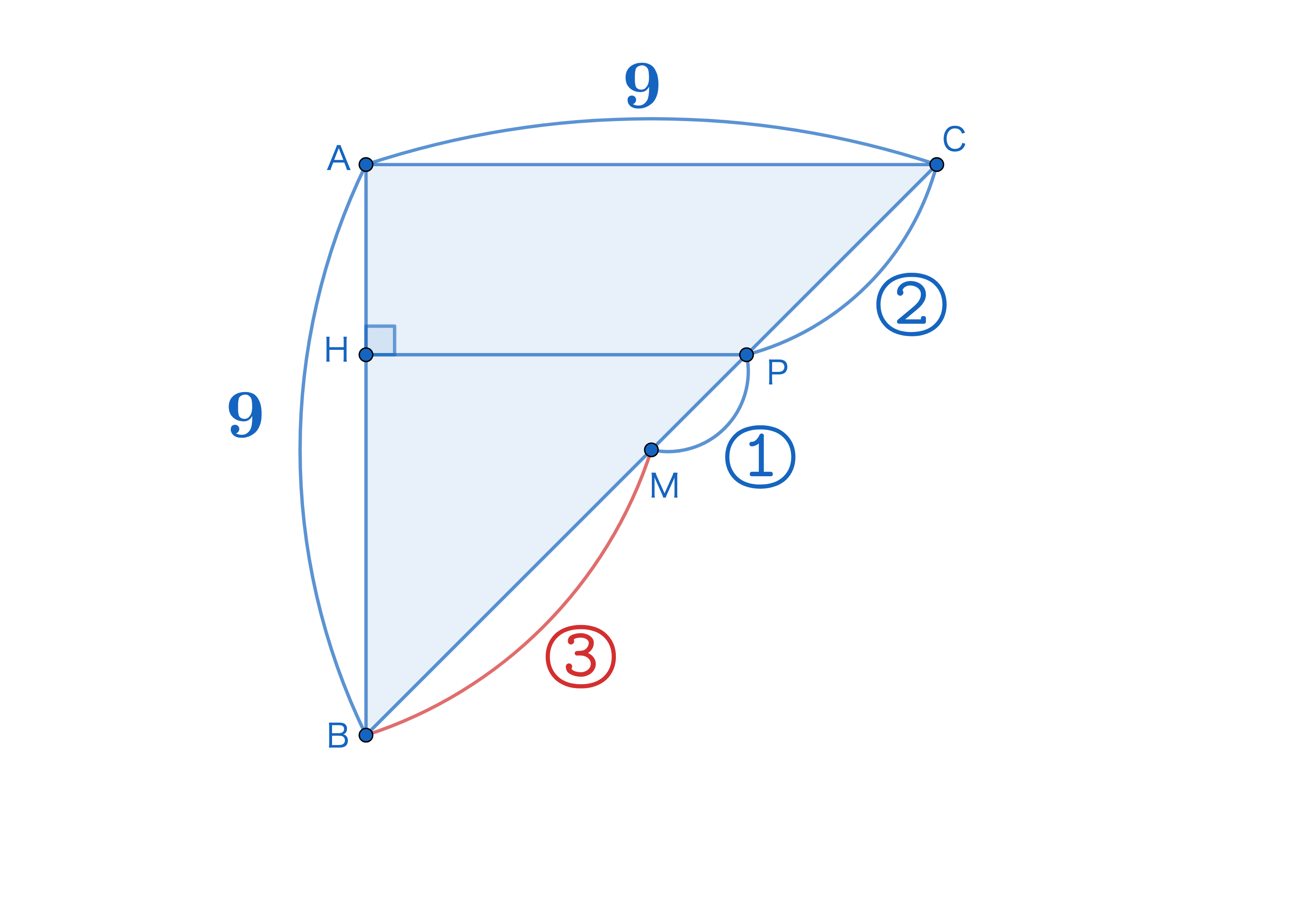
MがBCの中点であることから、MP=①とした比でBMを表すとBM=③となる。ここで△ABC∽△HBPなので、
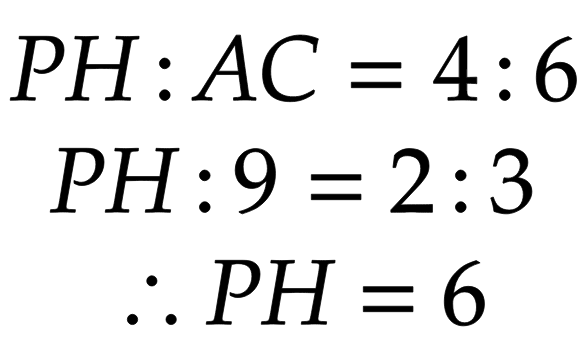
よって求めたい体積は、
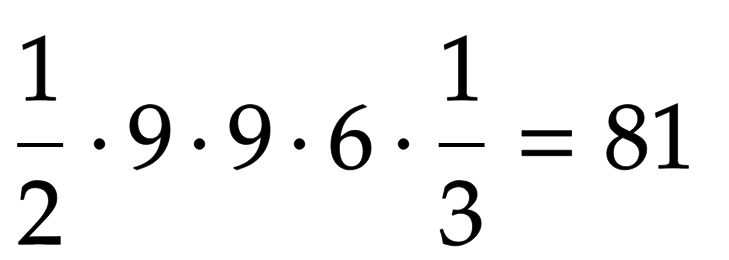
違う視点からみて高さを求める、というのもセオリーなのでこの問題は第4問の問2に比べると簡単ですね。答えも約分されて整数になるので計算も簡単です。
ということで、2019年の都立高校入試、数学の解説でした。ちなみに私は神奈川県の生徒も多く指導しているので、神奈川県の入試問題もチェックしてます。数学に関しては神奈川県の問題の方がはるかに難しかったので、興味がある人は以下の記事もご覧ください（一番難しかった問題の解説記事だけ載せておきます）。
神奈川県公立高校入試、都立高校入試、大学入試で個別指導18年、オンライン指導8年の私がマンツーマンで丁寧に指導します。
- 対象学年：中学生、高校生、浪人生
- 指導科目（高校）：数学、物理、大学受験指導
- 指導科目（中学）：数学、理科、高校受験指導
- 指導形態：SkypeまたはZoomによるオンライン指導
- 指導曜日・時間：要相談
- 料金：1時間6,000円（税別）→5,000円（2月3月指導開始の方だけ！）
- 体験指導：60分（ヒアリング含む）
体験指導をご希望の方、オンライン指導に関してご質問がある方は以下のお問い合わせページからご連絡ください。体験指導や指導料金などについて詳しい資料をお送りします。
